U379473 星月树
题目背景
>仙人种下了日之种,其生出了月之枝。流星划过长空,却又被枝条捕获,化为星之果。
题目描述
兔替仙人看护星月树。
星月树的月之枝被编号为 $l_0,l_1,\dots,l_{\operatorname len(l)-1}$ ,
星之果被编号为 $a_0,a_1,\dots,a_{\operatorname len(a)-1}$ 。( $\operatorname len(g)$ 表示序列 $g$ 的长度)。
最初,星月树上有 $M$ 根月之枝,所有月之枝上没有一颗星之果,世界时数 ${T}$ 为 $0$,世界常数是 $k$ 。
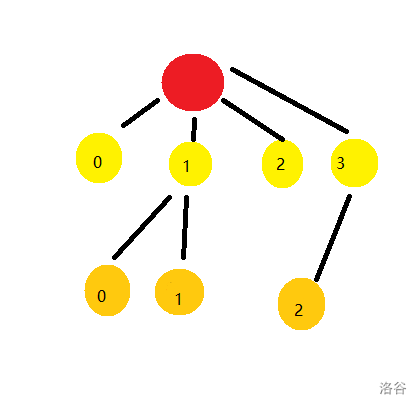
如图是一颗 $M=4$ 的初始星月树:
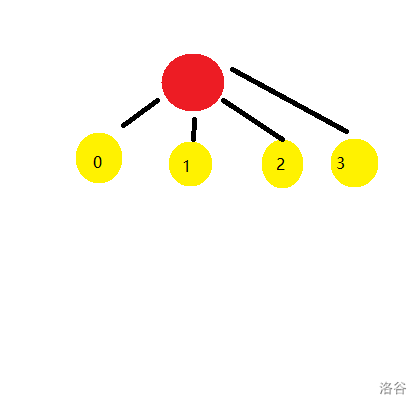
在第 $i(1\le i\le N)$ 天,兔会做两件事:
1. 观测到星月树发生的变化 **(记为 $d_i$ )**
- $d_i = 0$ 表示无事发生。
- $d_i = 1$ 表示一颗大小为 **$b_i$** 流星被编号 **$m_i$** 的月之枝捕获,放于编号为 $s_i$ 的星之果之后 **(此时,被捕获的星之果编号为 $s_{i+1}$ ,功效为 $(b_i+Tk)\bmod p_1$ ,保证 $m_i,s_i$ 存在且 $s_i$ 生长在 $m_i$ 以左(或者就是生长在 $m_i$ 上),操作后 $s_i$ 不变,)。**
注:
1. 如果 $s_i=-1$,则在 $s_0$ 左侧插入。若 $s_0$ 不存在,则直接放入 $m_i$ 下(见图)。
2. 当 $\operatorname len(a)=0$时,必定第一次 $d_i=1$ 的操作的 $s_i=-1$ 。
如图是在上图的情况下,在 $1$ 号月之枝上抓捕流星($s_i=-1$)时的情况:
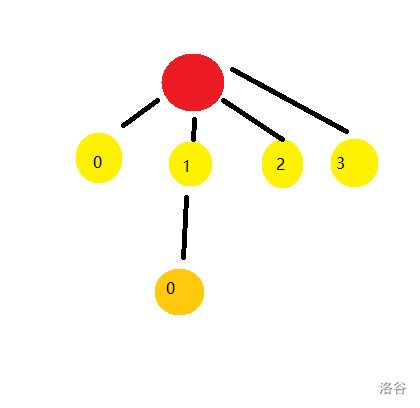
现在,在 $2$ 号月之枝处抓捕一颗流星($s_i=0$):
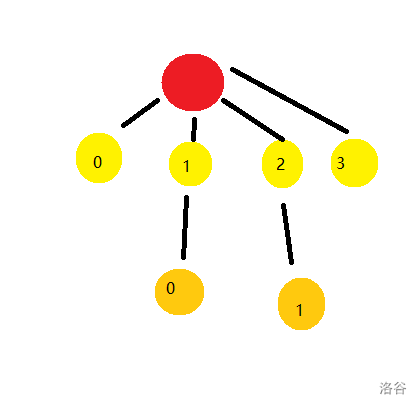
在 $1$ 号月之枝上抓捕一颗流星($s_i=-1$):
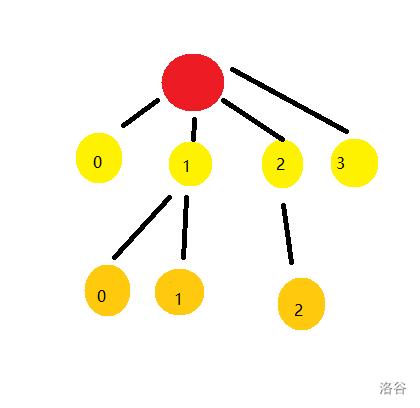
- $d_i = 3$ 表示一支月之枝 **(记为 $f_i$ )** 将自己的一部分星之果 **(记为 $[u_{1_i},d_{1_i}]$ )** 给另外一支月之枝 **(记为 $t_i$ )** **(保证 $f_i,u_{1_i},d_{1_i},t_i$ 存在且 $u_{1_i}\leq d_{1_i}$ ,同时,设 $t_i$ 拥有的星之果为 $[u_{2_i},d_{2_i}]$ ,则两个区间相邻且 $[u_{1_i},d_{1_i}]$ 在 $f_i$ 上)** 。
**注:可能存在 $u_{1_i}=d_{1_i}$。**
如下图,$f_i=2$,区间为$[2,2]$,$t_i=3$。
2. 研究星月树的性质(记为 $w_i$ )。
- $w_i = 0$ 表示休息,不做研究 **(输出 `null` , $T$ 不变)**。
- $w_i = 1$ 表示求月之枝 $m_i$ 上的星之果个数 **(输出答案 $ans_i\bmod p_2$ )( $T=(T+ans_i)\bmod p_1$ )** 。
- $w_i = 3$ 表示求星之果 $s_i$ 的功效 **(输出答案 $ans_i\bmod p_2$ )( $T=(T+ans_i)\bmod p_1$ )**。
你是兔的助手,请为了兔,为了仙人,为了星月树,~~为了AC,~~ 写一个代码吧~
>那就是希望。
>
>即便需要取模,也是光明。
>
> ——P5291 [十二省联考 2019] 希望
输入格式
第一行五个整数 $N,M,p_1,p_2,k$ ,含义如题意所释。
接下来 $N$ 组数据,每组数据两行:
第一行,首先一个整数 $d_i$ 。
- $d_i = 0$ 时无附加数据。
- $d_i = 1$ 时三个整数 $b_i,m_i,s_i$ 。
- $d_i = 3$ 时四个整数 $f_i,u_{1_i},d_{1_i},t_i$ 。
第二行,首先一个整数 $w_i$ 。
- $w_i = 0$ 时无附加数据。
- $w_i = 1$ 时一个整数 $m_i$ 。
- $w_i = 3$ 时一个整数 $s_i$ 。
输出格式
一共 $N$ 行,如题意所释。
说明/提示
对于所有测试数据有:
$1 \leq N \leq 10^6,1\leq M \leq N,0\leq k\leq 10,2\leq p_1,p_2\leq10^8,0\leq b_i\leq10^9,0\leq d_i,w_i\leq 3 $ 。
| 测试点 | $N\leq$ | 特殊性质 |
| :----------: | :----------: | :----------: |
| $1\sim 3$ | $10^4$ | 无 |
| $4\sim 5$ | $10^6$ | A |
| $6\sim 8$ | $10^6$ | B |
| $9\sim 15$ | $10^6$ | 无 |
特殊性质 A:$k=0$。
特殊性质 B:$w_i=0$或$w_i=3$