U458535 Tree Game
题目背景
$Beaver$ 和 $Revaeb$ 之间长达一个世纪的竞争一直持续到今天。这一次,他们决定在多人游戏中挑战对方。

题目描述
有 $1$ 只 $Beaver$ 和 $m$ 只 $Revaeb$ 参与了游戏,游戏失败的 $Revaeb$ 要被拉出去和 $Bevaeb$ 贴贴。
$Beaver$ 是游戏的裁判,由于所有 $Revaeb$ 都想和 $Beaver$ 贴贴,于是 $Beaver$ 要淘汰所有的 $Revaeb$ 。下面是 $Beaver$ 淘汰 $Revaeb$ 的方式:
- 有一棵 $n$ 个结点的无根树,每只 $Revaeb$ 都有两个特殊结点 $x_i$ 与 $y_i$。
- 在一次操作中,$Beaver$ 可以选择某个结点 $v$。接下来,对于所有未被淘汰的 $Revaeb$ $i$,$Beaver$ 将找到一个结点 $w$,满足其在 $x_i$ 到 $y_i$ 的简单路径上且距离 $v$ 最近,若 $w\neq x_i$ 且 $w\neq y_i$,那么 $Revaeb$ $i$ 将会被淘汰。
现在 $Bevaeb$ 想要知道至少要进行多少次操作才能淘汰所有的 $Revaeb$。如果无论如何都不能淘汰所有的 $Revaeb$,请输出 $-1$。
输入格式
**注意:本题采用多组数据。**
第一行一个正整数:$T$,表示数据组数;
接下来 $T$ 组数据,对于每一组数据:
第一行含两个数 $n$ 与 $m$,意义同上所述。
第二行含 $n-1$ 个数 $par_2,par_3,\dots,par_n$,其中 $par_i$ 代表无根树上存在一条连接 $i$ 与 $par_i$ 的边。
接下来 $m$ 行,第 $i$ 行含两个数 $x_i$ 与 $y_i$,意义同上所述。
输出格式
对于每一组数据:
若有解输出最小次数;
否则输出 ```-1```。
说明/提示
**【样例解释】**
第一个样本的说明:
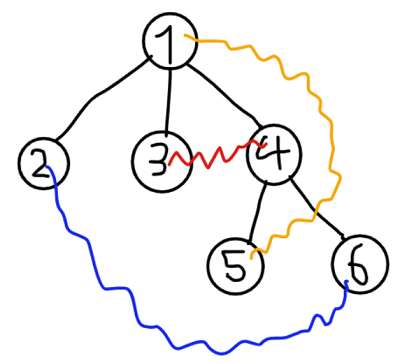
在第一次操作中,$Beaver$ 可以选择顶点 $1$ 并消除红色和蓝色的棋手。在第二次操作中,他可以选择顶点 $6$,并消除颜色为橙色的棋手。
在第二个示例中,$Beaver$ 无法消除第一个玩家。
**【数据范围】**
对于所有测试数据保证:$T\le 10^5,\sum n,\sum m\le 3\times 10^5,1\le par_i< i$。
| 测试点编号 | $\sum n\leq$ | $m\leq$ | 特殊性质或约束 |
| :----------: | :----------: | :----------: | :----------: |
| $1,2$ | $15$ | $15$ | \ |
| $3,4$ | $100$ | $20$ | \ |
| $5,6,7$ | $300$ | $300$ | \ |
| $8,9,10$ | $1000$ | $1000$ | \ |
| $11,12,13,14$ | $3\times 10^5$ | $3\times 10^5$ | $par_i=1$ |
| $15,16,17,18$ | $3\times 10^5$ | $3\times 10^5$ | $par_i=i-1$ |
| $19,20,21,22,23,24,25$ | $3\times 10^5$ | $3\times 10^5$ | \ |