U511581 蛇蛇放置

小 C 在和小 P 在一个 $n \times m$ 的棋盘上玩一种贪吃蛇变种。这种贪吃蛇很特别，没有头尾之分，它的头尾统称为端点，它所占的棋盘格数称为它的长度。 小 P 在棋盘上摆了很多条长度为 $1$ 的蛇。在每一回合，小 C 会随机选择两个相邻的端点，并将这两个端点对应的贪吃蛇首尾相接，融合成一条新的蛇。 特别地，如果小 C 选择的两个端点属于同一条蛇，那么它会变成一条「衔尾蛇」。遗憾的是，「衔尾蛇」不被「宇宙规则」所认可，为了不被「宇宙规则」制裁，如果出现了「衔尾蛇」，小 C 就会把棋盘清空。 小 C 将会操作足够多的回合，直到无法再操作（也就是说棋盘上不存在相邻的端点）时游戏结束。 小 C 想请你求出：对于小 P 指定的初始状态，游戏结束之后能够形成多少种不同的局面。答案对 $10^9+7$ 取模。

第一行两个整数 $n, m$。 接下来 $n$ 行，每行 $m$ 个字符，若字符为 $\texttt{x}$，则表示小 P 在这一格放了一条长度为 $1$ 的蛇，若字符为 $\texttt{.}$ 则没有蛇。

一行一个整数，最终局面的种数，答案对 $10^9+7$ 取模。

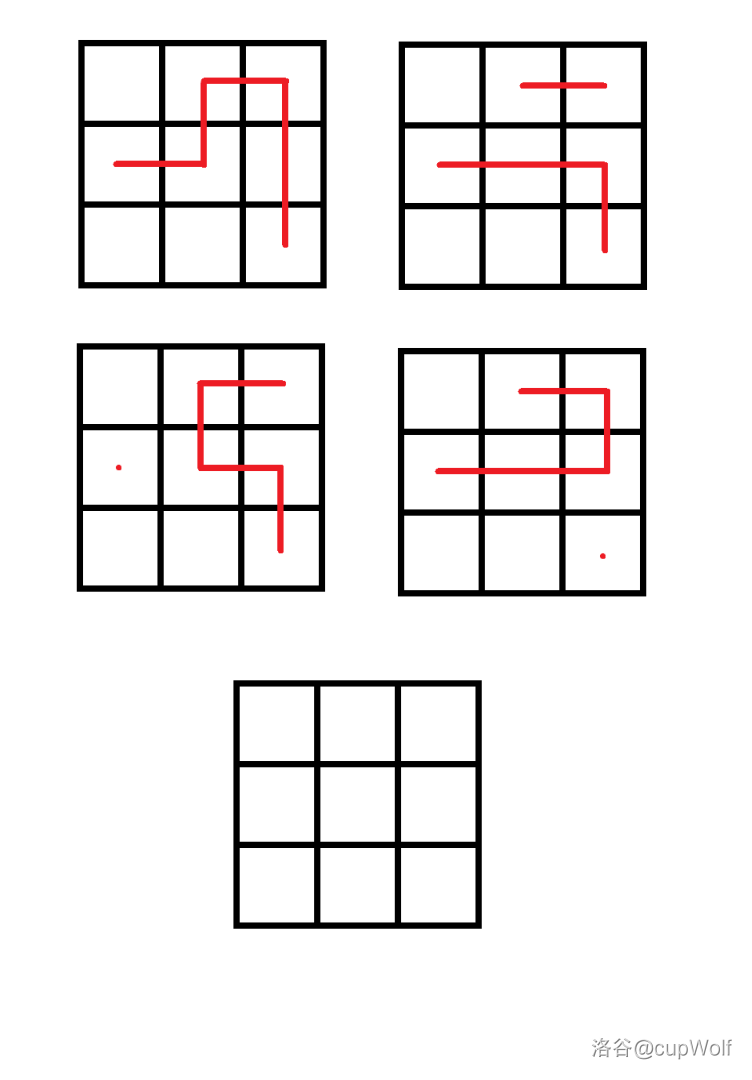
**请注意：空状态也算一种状态。** ### 样例解释 1 无论如何操作，当棋盘上只剩一条蛇的时候，这条蛇的头尾必定相邻，然后在下一个回合形成衔尾蛇。因此，无论小 C 如何操作，棋盘都会被清空。 ### 样例解释 2 $5$ 种最终局面分别是：  ### 数据范围 对于 $100\%$ 的数据，$1 \le n, m \le 12$。