U533311 2.8 二分图讲题

## 前置知识 - 图论基础概念及算法 ## 一、二分图引入 定义节点 $V$ 由两个集合 $X,Y$ 组成，且 **两个集合内部没有边的图** 是二分图。 容易发现它的两个性质： - 二分图可以进行黑白染色。 - 二分图不存在长度为奇数的环。 于是，为了判定一个图是不是二分图，我们只需要尝试对它进行黑白染色即可。 给出示例代码： ```c++ void dfs(int x, int color) { col[x] = color; for (int i = 0; i < vec[x].size(); i++) { int v = vec[x][i]; if (!col[v]) dfs(v, 3 - color); else if (col[v] == col[x]) {ans = 0; return ;} if (!ans) return ; } } // in main for (int i = 1; i 证明：（from [OI-wiki 二分图最大匹配-二分图最小点覆盖（König 定理）](https://oi-wiki.org/graph/graph-matching/bigraph-match/#%E4%BA%8C%E5%88%86%E5%9B%BE%E6%9C%80%E5%B0%8F%E7%82%B9%E8%A6%86%E7%9B%96k%C3%B6nig-%E5%AE%9A%E7%90%86)） > > 将二分图点集分成左右两个集合，使得所有边的两个端点都不在一个集合。 > > 考虑如下构造：从左侧未匹配的节点出发，按照匈牙利算法中增广路的方式走，即先走一条未匹配边，再走一条匹配边。由于已经求出了最大匹配，所以这样的「增广路」一定以匹配边结束，即增广路是不完整的。在所有经过这样「增广路」的节点上打标记。则最后构造的集合是：所有左侧未打标记的节点和所有右侧打了标记的节点。 > > 首先，这个集合的大小等于最大匹配。左边未打标记的点都一定对应着一个匹配边（否则会以这个点为起点开始标记），右边打了标记的节点一定在一条不完整的增广路上，也会对应一个匹配边。假设存在一条匹配边左侧标记了，右侧没标记，左边的点只能是通过另一条匹配边走过来，此时左边的点有两条匹配边，不符合最大匹配的规定；假设存在一条匹配边左侧没标记，右侧标记了，那就会从右边的点沿着这条匹配边走过来，从而左侧也有标记。因此，每一条匹配的边两侧一定都有标记（在不完整的增广路上）或都没有标记，匹配边的两个节点中必然有一个被选中。 > > 其次，这个集合是一个点覆盖。由于我们的构造方式是：所有左侧未打标记的节点和所有右侧打了标记的节点。假设存在左侧打标记且右侧没打标记的边，对于匹配边，上一段已经说明其不存在，对于非匹配边，右端点一定会由这条非匹配边经过，从而被打上标记。因此，这样的构造能够覆盖所有边。 > > 同时，不存在更小的点覆盖。为了覆盖最大匹配的所有边，至少要有最大匹配边数的点数。 ### 习题：[ACWing 376. 机器任务](https://www.acwing.com/problem/content/378/) & [UVA1194 Machine Schedule](https://www.luogu.com.cn/problem/UVA1194) 如果一个任务 $i$ 可以使用 $A$ 的 $x$ 模式或 $B$ 的 $y$ 模式，将左部点 $x$ 向右部点 $y$ 连边。最终我们需要选出一些点覆盖所有的边，即求出最小点覆盖集。 由上述定理，容易求解。实现略。 ## 点独立集 点独立集：从无向图 $G(V,E)$ 中选取一个顶点集合 $V'\subseteq V$，其中任意两个顶点之间不相邻，则称 $V'$ 为无向图 $G$ 的一个点独立集。 最大点独立集：图中顶点数最多的一个点独立集。 - 对二分图，有定理：**$|$ 最大点独立集 $|=$ 顶点总数 $-|$ 最大匹配 $|$**。 证明略。 ### 习题：[HDU1068 Girls and Boys](https://vjudge.net/problem/HDU-1068) 找出最多的人，使得两两间没有关系，即求出最大点独立集。 由上述定理，容易求解。实现略。 ### 经验：[P6268 [SHOI2002] 舞会](https://www.luogu.com.cn/problem/P6268) ## 边覆盖集 边覆盖集：从无向图 $G(V,E)$ 中选取一个边集 $E'\subseteq E$，满足图中任意一个顶点都与边集 $E'$ 中的其中一条边相关联，则称 $E'$ 是 $G$ 的一个边覆盖集。 最小边覆盖集：图中边数最少的一个边覆盖集。 **注意：边覆盖集的定义仅在原图中不存在孤点的时候才成立。否则无解**。 - 对二分图，有定理：**$|$ 最小边覆盖集 $|=$ 顶点总数 $-|$ 最大匹配 $|$**。 证明略。 ### 习题：[ACWing 372.棋盘覆盖](https://www.acwing.com/problem/content/374/) & [POJ2446 Chessboard](https://vjudge.net/problem/POJ-2446) 使用 $1\times2$ 的纸片覆盖一个有孔的棋盘，则将棋盘黑白染色，相邻的黑白点之间连边。想要覆盖整个棋盘，必须每个位置都连上一条边，即求出最小边覆盖集。 由上述定理，容易求解。实现略。 ## 边独立集 边独立集：从无向图 $G(V,E)$ 中选取一个边集 $E'$，其中任意两条边之间不相邻，则称 $E'$ 为无向图 $G$ 的边独立集。 最大边独立集：图中边数最多的一个边独立集。 - 对二分图，有定理：**$|$ 最大边独立集 $|=|$ 最大匹配 $|$**。 这是二分图最大匹配的定义。 ### 习题：[P3386 【模板】二分图最大匹配](https://www.luogu.com.cn/problem/P3386) 大道至简。由上述定理，容易求解。实现略。 ## 路径覆盖 路径覆盖：在 **有向图** 中，找到若干条路径，使之覆盖了图中的所有顶点，并且任何一个顶点都只出现在一个路径中。 最小路径覆盖：图中路径数最少的路径覆盖。 我们来详细解释一下怎么求最小路径覆盖。对于一张 DAG 上的每一个点，将其拆成“入点”和“出点”两个点。如果原图上 $x$ 个 $y$ 之间连有一条有向边，则用 $x$ 的出点向 $y$ 的入点连一条边。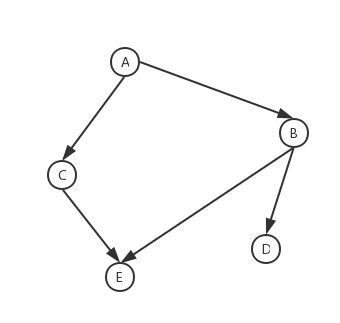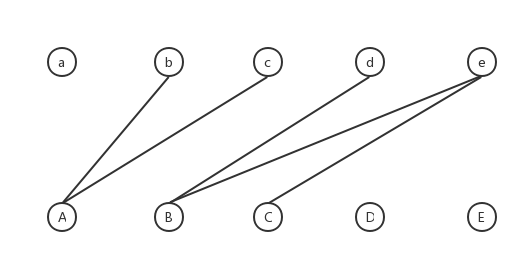   容易发现，新图构成一张二分图。 - 对 **DAG**，有定理：**$|$ 最小路径覆盖 $|=$ 顶点总数 $-|$ 最大匹配 $|$**。 > 虽迟但到的证明： > > 路径覆盖中的每条简单路径除了最后一个节点之外都有唯一的后继和它对应，因此匹配边的条数就是非路径结尾的节点数。当匹配数量达到最大时，非路径结尾的节点数达到最大，此时结尾点数量最小，即路径数最小。 ### 习题：[UVA1184 Air Raid](https://www.luogu.com.cn/problem/UVA1184) 模板题。容易发现题意就是求最小路径覆盖。 由上述定理，容易求解。实现略。 ### 习题：[51NOD 1392 装盒子](https://vjudge.net/problem/51Nod-1392) 可以将相互存在包含关系的盒子之间连有向边（**注意：不要连出环来，该算法仅对 DAG 有效**），然后我们可以将盒子 **按大小从大到小排序**，然后依次尝试寻找匹配即可。容易发现，存在于匹配中的边对应的点必然面积更大，而它们会被删去，剩下的面积就一定是最小的。 ## 本节小结 上面我们对二分图常见的性质定理进行了简单的介绍。下面我们用表格的形式对上述定理做一个总结。 |名称|定理| |:-:|:-:| |最小点覆盖集|$\mid$ 最小点覆盖集 $\mid=\mid$ 最大匹配 $\mid$| |最大点独立集|$\mid$ 最大点独立集 $\mid=$ 顶点总数 $-\mid$ 最大匹配 $\mid$| |最小边覆盖集|$\mid$ 最小边覆盖集 $\mid=$ 顶点总数 $-\mid$ 最大匹配 $\mid$| |最大边独立集|$\mid$ 最大边独立集 $\mid=\mid$ 最大匹配 $\mid$| |最小路径覆盖|$\mid$ 最小路径覆盖 $\mid=$ 顶点总数 $-\mid$ 最大匹配 $\mid$| ## 四、让我们来构造！ ### 最大边独立集 跑二分图匹配模板，自然求出一组解。 ### 最小边覆盖集 先求出一组最大匹配，所有匹配点均采用与其相连的匹配边；为非匹配点连任意一条边即可。 ### 最小点覆盖集 设当前二分图为 $G=$，已经找到的匹配为 $M$。 从 $Y$ 点集的一个非匹配点出发，循着“非匹配边 $\to$ 匹配边 $\to$ 非匹配边 $\to$ 匹配边……”的原则走下去（可能会有多条路径），沿途标记所走过的点，最后结束的位置一定是“匹配边”（因为 $M$ 是最大匹配，不存在增广路），并且结束点在 $Y$ 点集中。 重复上述过程，直到 $Y$ 点集的非匹配点都被标记。我们记 $X$ 点集中 **已标记的点** 和 $Y$ 点集中 **未标记的点** 的集合为 $S$，则 $S$ 为最小点覆盖集。 > 证明：（了解即可） > > - 因为 $Y$ 点集中，所有非匹配都被标记了，没被标记的点一定对应一条匹配边，而 $X$ 点集中已标记的点也一定对应匹配边，所以 $S$ 中每个点都会对应一条匹配边。下面说明对应的匹配边不会重复。 > > - 根据上述构造方法，很容易得到下面两个结论： > > 1. 一条匹配边如果在 $X$ 点集中的点被标记，那么在 $Y$ 点集中的点一定被标记。 > > 2. 一条匹配边如果在 $Y$ 点集中的点没被标记，那么在 $X$ 点集中的点一定没被标记。 > > - 所以一条匹配边要么两边都被标记，要么两边都没被标记。因此，$S$ 中每个点都和一条匹配边一一对应，不会有重复对应的情况，也就是 $|S|=|M|$。 > > - 要证明 $S$ 为覆盖集，也就是证明不存在一条边在 $X$ 点集中的点未标记，在 $Y$ 点集中的点已标记。 > > 首先匹配边两边的标记情况是相同的，肯定不会出现这种情况，只需要考虑非匹配边。而考虑非匹配边的时候，只需要考虑在 $Y$ 点集中的那个端点是非匹配点，在 $X$ 点集中的那个端点是匹配点（都是非匹配点就和最大匹配矛盾了），那从 $Y$ 点集中的端点出发一定会有路径经过在 $X$ 点集中的端点，就会被标记了，所以这种情况是不存在的。 > > 所以 $S$ 是覆盖集。 > > 我们至少要 $|M|$ 个点才能把所有匹配边的覆盖（因为匹配之间没有公共点），因此 $|$ 最小点覆盖集 $|\ge|M|$。 > > 综上，$S$ 为最小覆盖集，且 $|S|=|M|$。证毕。 具体实现采用 dfs。 ### 习题：[UVA11419 SAM I AM](https://www.luogu.com.cn/problem/UVA11419) 模板的最小点覆盖问题。下面是示例代码，展示了如何采用 dfs 进行具体方案的求解。 ```c++ #include #include using namespace std; const int MAX_N = 1005; const int MAX_M = 1000005; struct Edge { int v, next; } e[MAX_M]; int p[MAX_N], eid; void init() { memset(p, -1, sizeof(p)); eid = 0; } void insert(int u, int v) { e[eid].v = v; e[eid].next = p[u]; p[u] = eid++; } bool rvis[MAX_N], lvis[MAX_N]; int rmatch[MAX_N], lmatch[MAX_N]; bool dfs(int u) { for (int i = p[u]; i != -1; i = e[i].next) { int v = e[i].v; if (!rvis[v]) { rvis[v] = true; if (rmatch[v] == -1 || dfs(rmatch[v])) { rmatch[v] = u; lmatch[u] = v; return true; } } } return false; } int hungary(int n) { int res = 0; memset(lmatch, -1, sizeof lmatch); memset(rmatch, -1, sizeof rmatch); for (int i = 1; i n >> m; init(); for (int i = 0; i < m; i++) { int u, v; cin >> u >> v; insert(u, v); } cout

输入两个整数 $a,b$，输出它们的和。

两个整数 $a,b$。

一个整数，表示结果。

### 数据范围 $-10^{18}\le a,b\le10^{18}$。