U534154 正三角形(triangle)(T1)
题目背景
$\ \ \ \ \ \ $作为一名数学爱好者,LHRG李 某天忽然心血来潮,想请你帮他计算一下一个大正三角形中**所有正三角形**的面积和。
题目描述
$\ \ \ \ \ \ $设每个**最小**的**最基本**的**小正三角形**的面积为$1$。
举例说明:
- 一层三角形:只有一个正三角形,面积为一,面积和为一。
- 两层三角形:一个大正三角形被分成四个小正三角形,有四个面积为一的小正三角形(三正一倒),有一个由四个小正三角形组成的面积为四大正三角形,面积和为八。
- 三层三角形:一个大正三角形被分成九个小正三角形,有九个面积为一的小正三角形(六正三倒),有三个由四个小正三角形组成的面积为四正三角形,有一个由九个小正三角形组成的面积为九的大正三角形,面积和为三十。
$\ \ \ \ \ \ $由于因为层数过多可能导致面积和过大,所以,请输出**面积和**对 $100000009$ 取模后的结果。
输入格式
一个整数,层数 $n$。
输出格式
取模后的**总面积和**。
说明/提示
数据范围:
| 子任务 | 测试点编号 | 总分数 | 数据范围 |
| :----: | :----: | :----: | :----: |
| **Subtask #1** | $1-2$ | 20 | $1\leqslant n \leqslant 100$ |
| **Subtask #2** | $3-5$ | 30 | $1\leqslant n \leqslant 10000$ |
| **Subtask #3** | $6-10$ | 50 | $1\leqslant n \leqslant 10^7$ |
对于$100\%$的数据,$1\leqslant n \leqslant 10^7$
样例一解释:
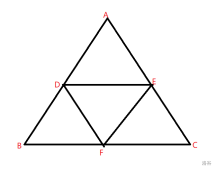
$S_{总}=S_{ \triangle ADE}+S_{ \triangle DBF}+S_{ \triangle EFC}+S_{ \triangle DEF}+S_{ \triangle ABC}=1+1+1+1+4=8$
样例二解释:
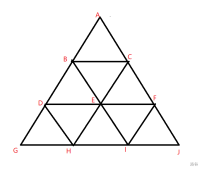
$S_{总}=S_{ \triangle ABC}+S_{ \triangle DBE}+S_{ \triangle BCE}+S_{ \triangle CEF}+S_{ \triangle DGH}+S_{ \triangle DEH}+S_{ \triangle EHI}+S_{ \triangle EFI}+S_{ \triangle FIJ}+S_{ \triangle ADF}+S_{ \triangle BGI}+S_{ \triangle CHJ}+S_{ \triangle AGJ}$
$\ \ \ \ \ =1+1+1+1+1+1+1+1+1+4+4+4+9$
$\ \ \ \ \ =30$
**友情提示:注意内存限制!**
[题解](http://lhrg.github.io/题解-U534154-【正三角形】/)
------------
出题者:LHRG李