U565580 GKK 的游戏

GKK 是一个喜欢环上游戏的男孩。 现在有一张 $n$ 个点组成的图，每个点的编号为 $0\sim n-1$。你有 $m$ 次操作，每一次操作有三个参数 $a,b,c$。操作的意义如下： * 在编号为 $a+0,b+0$ 的点之间连一条边权为 $c+0$ 的边。 * 在编号为 $b+0,a+1$ 的点之间连一条边权为 $c+1$ 的边。 * 在编号为 $a+1,b+1$ 的点之间连一条边权为 $c+2$ 的边。 * 在编号为 $b+1,a+2$ 的点之间连一条边权为 $c+3$ 的边。 * 在编号为 $a+2,b+2$ 的点之间连一条边权为 $c+4$ 的边。 * 在编号为 $b+2,a+3$ 的点之间连一条边权为 $c+5$ 的边。 * …… 其中，点的编号都是模 $n$ 意义下的，即 $n$ 号点与 $0$ 号点等价，$2n-1$ 号点与 $n-1$ 号点等价。 为了方便理解，下图为 $n=16,a=17,b=14,c=7$ 时首先加入的 $7$ 条边。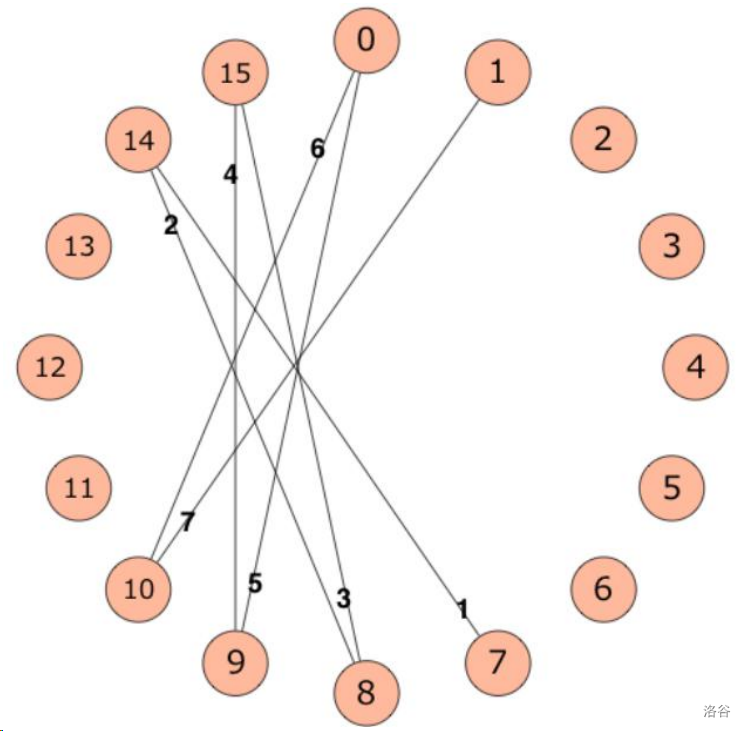  GKK 想知道，在所有操作进行完毕之后，图的最小生成树的各边权值之和。他把这个问题抛给了你。 最小生成树的定义：从 $n$ 个点的图中选出 $n-1$ 条边，使图联通且所选边的权值和最小。

第一行两个正整数 $n,m$ 表示点数和操作数。 接下来 $m$ 行，每行三个非负整数 $a,b,c$ 表示一次操作。

一行一个整数表示答案。

### 样例解释 #1 最小生成树如图，答案为 $1+2+3+4+5+6=21$。  ### 数据范围 对于 $100\%$ 的数据，满足 $2\leq n\leq 2\times 10^5,1\leq m\leq2\times10^5$。 ### 提示 1. 可能存在重边或自环。 2. 边权也许可以构成一个等差数列，公差为 $2$。