U604028 Vannies and 7

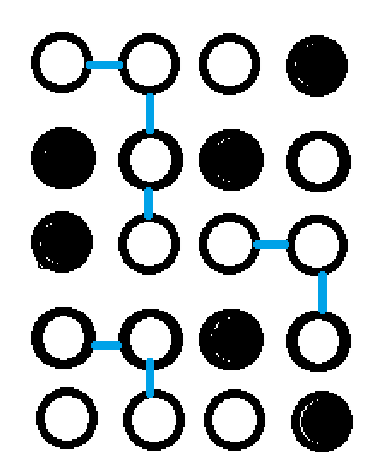
7 is vannies' favorite number! Vannies has a grid of $n\times m$ , and each cell is either black or white. He can connect some pairs of white cells using line segments of length $1$ , such that these segments only connect adjacent white cells (horizontally or vertically). Now Vannies wants to find the number of ways to form exactly three disjoint "7-shaped" figures. An "7-shaped" figure is a set of connected line segments intersecting at their right and top ends that form an "7" shape. The "7" shape cannot be rotated. See the example for better understanding. Note that the three figures need to be disjoint, that is no white cell should lie on two segments belonging to different figures. Two ways of connection are considered different if and only if the set of connecting line segments in two graphs are different(that is the order of operation is not important).

The first line contains two positive integers, $n$ and $m$, representing the number of rows and columns.($n,m\leq 30$) The next $n$ lines contain $m$ characters each, with . representing a white cell and # representing a black cell.

One number representing the number of ways to to form exactly three "7-shaped" figures.

The graph below is a valid way of connection.