U629413 库因兰德(Q Island)
题目背景
小红帽取出一面巨大的镜子,立在面前。“爱丽丝就在里面。”她说。
铃仙向前走去,如同穿过一层薄雾,进入了镜中。她发现自己站在一个巨大的游乐园里。天色是昏沉的,但所有的建筑自身都在发光,明亮又安静。空气温暖宜人,仿佛永远是夏天。
统治这里的赤之女王——普利凯特——坐在一个旋转茶杯上。铃仙走上前,向她询问爱丽丝的下落。
“我就是爱丽丝呀。”普利凯特女王说。
“这可真有意思,”铃仙在心里默默思量,“我虽然不认识爱丽丝,但我十分确信,她绝不是爱丽丝。”
女王似乎看透了她的心思。“好吧,”她有些遗憾地说,“如果你坚持要找那个‘爱丽丝’,我们可以玩个游戏。你从这个棋盘的一角走到另一角,我就告诉你她在哪儿。”
她顿了顿,补充规则:“你只能朝一个固定的方向前进。但棋盘上的每个法阵,要么会把你传送到别处,要么会改变你前进的方向。”
“那么,”女王用手指敲着棋盘,发出清脆的响声,“你能从(1,1)开始,坚持向右,最终走到(n,n)吗?”
题目描述
给定一个 $n×n$ 棋盘,棋盘中存在两类法阵:
- **传送法阵**:位于格子$ (a,b)$,若行进至此格子,则被直接传送到格子$ (x,y)$。
- **转向法阵**:位于格子 $(c,d)$,行进至此格子,则方向顺时针旋转 $90°$(若原本向右,则转向后向下)。
行进方向仅能通过转向法阵改变。初始位置为$ (1,1)$,初始方向为向右。
如果行进方向的下一步,将走到棋盘之外,则判定为永远无法到达
如果经过传送法阵,被传送到$ (x,y)$的格子,如果该格子上存在法阵,将立即执行该法阵的效果
传送法阵不会原地传送,即不会从$ (x,y)$的格子传送到$ (x,y)$的格子
保证一个格子不会出现一个以上的法阵,保证格子$(n,n),(1,1)$不存在法阵
问:是否能够通过一系列行进和法阵作用,最终到达格子$ (n,n)$?
输入格式
第一行包含一个正整数 $n$,表示棋盘的大小。
第二行包含一个正整数 $m$,表示传送法阵的数量。
接下来 $m$ 行,每行包含四个正整数 $a,b,x,y$,表示在格子$ (a,b)$ 有一个传送法阵,当行进至此格子时,会被传送到格子 $(x,y)$。
接下来一行包含一个正整数 $k$,表示转向法阵的数量。
接下来 $k$ 行,每行包含两个正整数 $c,d$,表示在格子 $(c,d) $有一个转向法阵,假设当行进至此格子且当前方向为右时,方向顺时针旋转 90°(即变为向下)。
对于$100\%$的数据,$n
输出格式
输出一行,如果能够到达格子 $(n,n)$,则输出 `YES`,否则输出 `NO`。
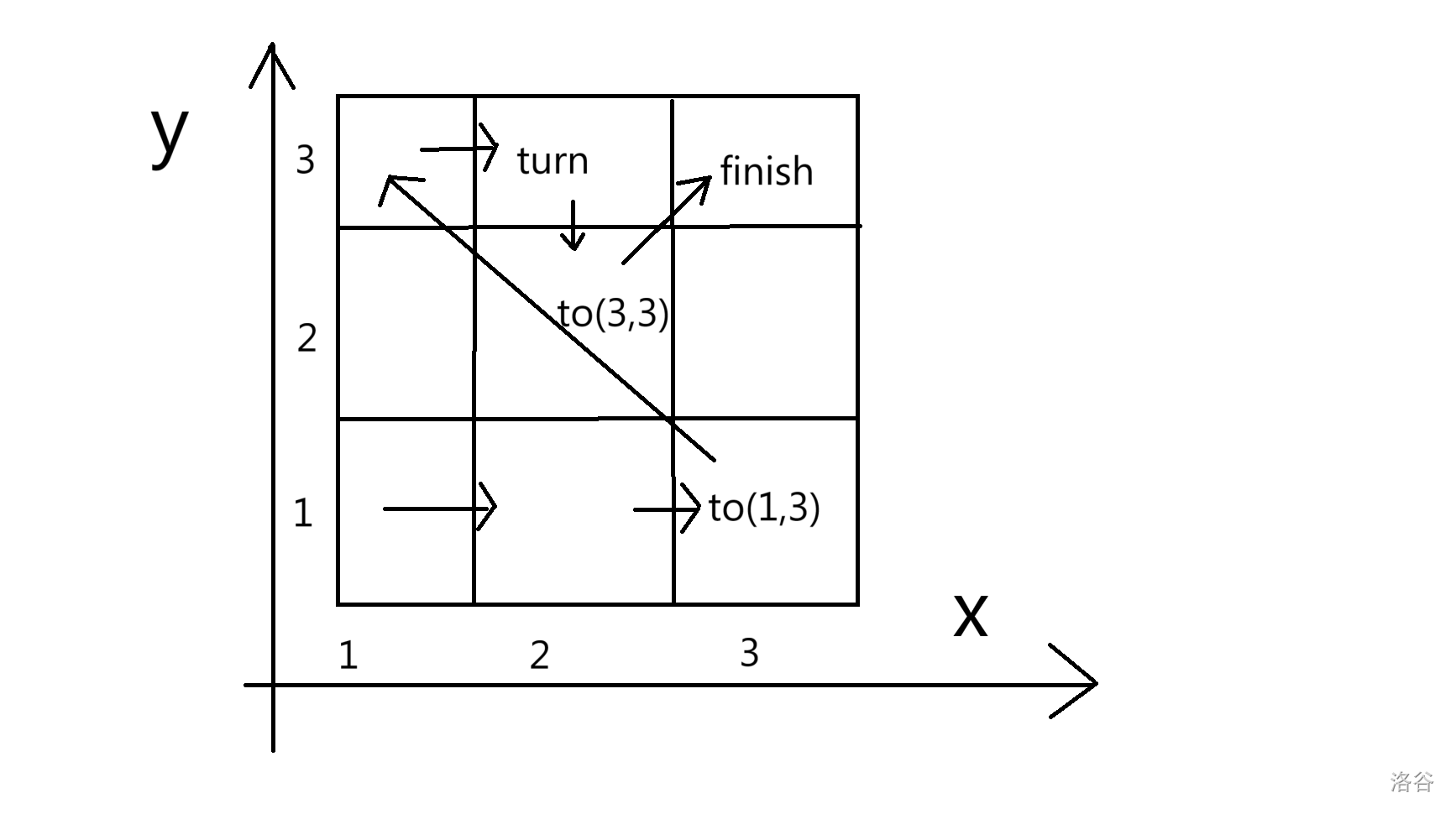
说明/提示
样例的解释