U635584 梦里看到的题（？）

出题人太菜了不会写 std，所以本题没有测试数据。 或许可以认为时限 1s，空间限制 512MB？

称连续子段为一个整数序列中满足子段中每个数都相等的子段。例如，对于 $[1,1,4,5,1,4]$，$[1]$ 是一个连续子段，而 $[1,1,4]$ 不是；这一序列的最长连续子段是 $[1,1]$。 以下记 $(u,v)$ 为 $u,v$ 两点间的链。 给定一棵有树，点有点权。你需要维护两种操作： * `1 u v x`，表示将 $(u,v)$ 上所有点的点权加上 $x$； * `2 u v`，表示询问将 $(u,v)$ 上所有点的点权按顺序写下后得到的序列的最长连续子段的长度。 **负整数在询问时可以视作任意正整数**，询问间互相独立。

第 $1$ 行输入一个正整数 $n$ 表示结点个数。 第 $2$ 行为 $n$ 个整数，第 $i$ 个整数 $v_i$ 表示 $i$ 号点的初始点权。 接下来 $n-1$ 行，每行两个正整数 $u,v$，表示树上存在一条连接 $u,v$ 的边。 然后一行一个正整数 $q$ 表示操作次数。 接下来 $q$ 行，每行代表一个操作，操作只有上述两种。

对于每个询问，输出一行一个正整数表示答案。

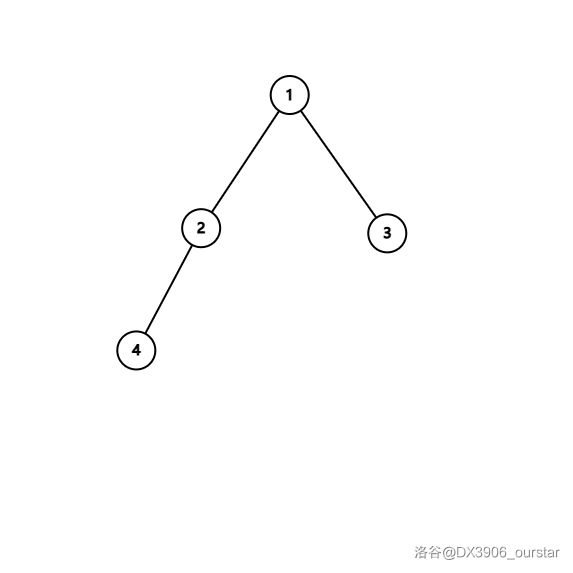
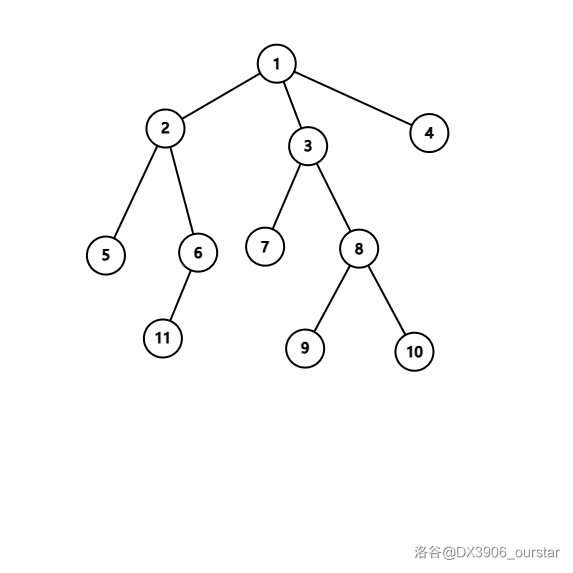
### 样例解释 样例 $1$ 的树长这样：  样例 $2$ 的树长这样：  在样例 $1$ 的第一组询问中，链上的点权依次为 $[1,1,4]$，其最长连续子段为 $[1,1]$。 在样例 $1$ 的第 $2$ 组询问中，链上的点权依次为 $[1,1,1]$，最长连续子段为 $[1,1,1]$。 在样例 $2$ 的第 $1 $组询问中，链上的点权依次为 $[-5,1,7,-2,3]$；一种可能的做法是将 $-5$ 看做 $1$，则 $[1,1]$ 构成最长连续子段。可以发现不存在更长的连续子段。 在样例 $2$ 的第 $2$ 组询问中，链上的点权依次为 $[1,8,8,-1]$；可以将 $-1$ 看做 $8$，则 $[8,8,8]$ 构成最长连续子段。可以发现不存在更长的连续子段。 ### 数据规模 * $1\le n,q\le 4\times 10^4$ * $-10^9 \le x,v_i \le 10^9$