U65320 Oak的预算方案

### 早在 $(({-1})^{2k(k\in N)}-\dfrac{1}{e^{i\pi}})$ 年前， **$Oak$** 便帮助金明解决了他的 **预算方案** 问题：

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 $N$ 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子： | $ $ **主件**$ $ $ $ $ $ | $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ **附件** $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ | | $ $ 电脑$ $ $ $ $ $ | 打印机，扫描仪 | | $ $ 书柜$ $ $ $ $ $ | $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ 图书 $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ | | $ $ 书桌$ $ $ $ $ $ | $ $ $ $ $ $ 台灯，文具 $ $ $ $ $ $ $ $ | | 工作椅 | $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ 无 $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ | 如果要买归类为附件的物品，必须先买该附件所属的主件。附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 $N$ 元。于是，他把每件物品规定了一个重要度，分为 $k$ 等：用整数 $1\sim k$ 表示，第 $k$ 等最重要。他还从因特网上查到了每件物品的价格。他希望在不超过 $N$ 元（可以等于 $N$ 元）的前提下，使每件物品的价格与重要度的乘积的总和最大。 设第 $j$ 件物品的价格为 $v[j]$ ，重要度为 $p[j]$ ，共选中了 $k$ 件物品，编号依次为 $j_1,j_2,...,j_k$ ，则所求的总和为： $v[j_1]\times p[j_1]+v[j_2]\times p[j_2]+...+v[j_k]\times p[j_k]$ ------------ **现在 $Oak$ 不满足于解决这类简单的问题(因为他需要购置满满一大卡车的物品)，于是他请你帮忙设计一个程序帮他处理那数据规模庞大的物品清单。**

第$1$行，为两个正整数，用一个空格隔开：$N\;m$（其中$N$表示总钱数，$m$为希望购买物品的个数。） 从第$2$行到第$m+1$行，第$i$行给出了编号为$i-1$的物品的基本数据，每行有$3$个非负整数 $v_{i-1}\;p_{i-1}\;q_{i-1}$ （其中$v_{i-1}$表示该物品的价格，$p_{i-1}$表示该物品的重要度，$q_{i-1}$表示该物品是主件还是附件。如果 $q_{i-1}=0$，表示该物品为主件，如果 $q_{i-1}>0$，表示该物品为附件，$q_{i-1}$是所属主件的编号）

一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值。

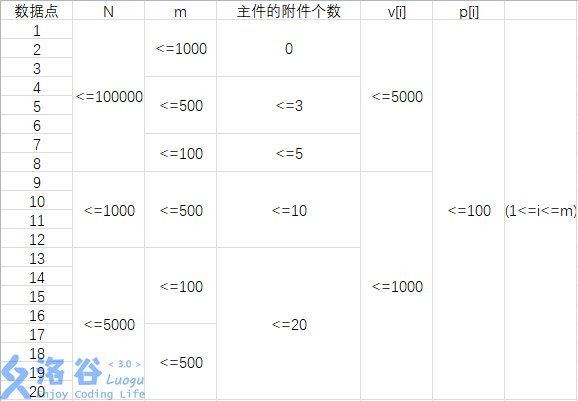
**数据范围：**  ------------ **样例解释：** ### 1：选择$4,5$号物品，此时所求总和为$400\times3+500\times2=2200$； ### 2：选择$1,7\sim20$号物品，所求总和为$35200$。 ------------ **提示：** ### 请注意时间和空间限制。 ### 可以使用$O_2$优化