UVA1017 快乐的轮子 Merrily, We Roll Along!
题目描述
测量路径长度的一种方法是滚动车轮(类似于自行车车轮),如果我们知道轮子的半径和它前进时的转数时,可以计算路径的长度。
如果路径平滑,此方法效果良好。但当有路缘或其他陡峭的海拔时,如果路径发生变化,可能无法准确确定路径距离,因为车轮可能会旋转车轮可能会围绕一个点(如路缘边缘)滚动,或者车轮可能会沿着垂直表面滚动。在这个问题上你要确定这样一个轮子的中心在沿着以下路径行进时移动的距离仅包括水平和垂直表面。
要测量路径,请将车轮放置在路径原点正上方的中心。然后,车轮在路径上尽可能地向前移动,始终保持其中心与表面位于路径末端的正上方。
考虑下图左侧所示的路径,并假设车轮有一个半径为$2$。路径以相同标高处长度为$2$的水平段开始和结束。之间在其他两个高度以下$2$个单位处,有一个长度为$2.828427$的水平段水平段。要测量此路径,请将车轮放置在位置$1$。然后,它水平移动到达位置$2$,旋转$45$度到达位置$3$,再旋转$45$度到位置$4$,最后滚动水平移动到位置5。轮子的中心移动了$7.1416$的距离,而不是$6.8284$。
在右图中,路径以水平长度段开始和结束。
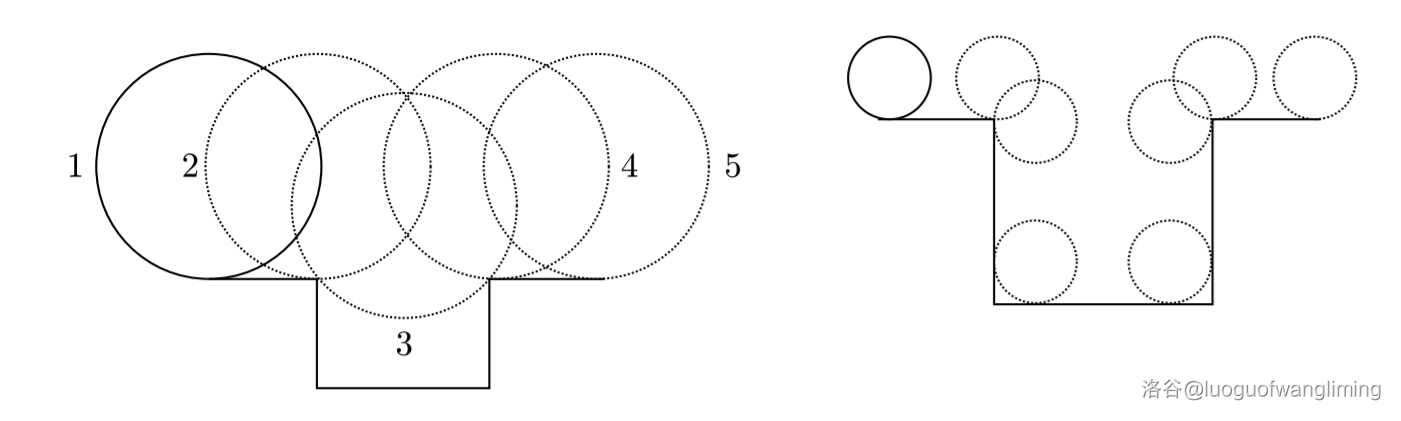
输入格式
**本题有多组数据**。
每组数据都以一个正实数开始,指定轮的半径和大于1小于50的整数$n$。接下来$n$对实数。每对中的第一个数字表示沿路径的水平距离到下一个垂直表面。每对中的第二个数字表示标高的有符号变化垂直表面上的路径,正数表示高度的增加。这个垂直表面总是垂直于水平表面。第$n$天的高度变化配对将始终为$0$。
第一个和最后一个水平段的长度都将严格大于半径。期间,圆永远不会同时与两个垂直段相切。
输入以一对零结束。
输出格式
对于每组数据,保留3位小数后显示数据编号和车轮中心移动的距离。