UVA10384 推门游戏 The Wall Pushers
题目描述
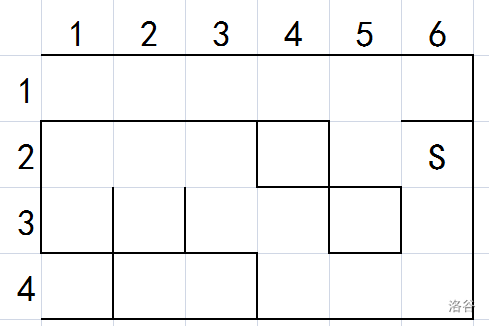
给你一个 $4\times 6$ 的网格图,网格边缘上可能有墙,如图:(实线即为墙)

对于每一个网格有一个权值 $val$,其中:
$$\begin{aligned}val= &\quad \ 1(\text{如果这个网格左边缘(西边缘)有墙})\\ &+2(\text{如果这个网格上边缘(北边缘)有墙})\\&+4(\text{如果这个网格右边缘(东边缘)有墙})\\&+8(\text{如果这个网格下边缘(南边缘)有墙})\end{aligned}$$
然后你就可以通过这些网格的权值唯一确定这张网格图了。
然后题目还会给你一个起点坐标 $(S_x,S_y)$**(注意,题目给的 $S_x$、$S_y$ 是坐标,不是行列,所以图中的 $S$ 点的坐标为 $(2,3)$)**,然后你从这个起点开始走,每步你可以往上下左右四个方向移动一格,但有限制条件。
具体来讲,假设你当前所在格子为 $(x,y)$,移动方向为 $dir$ ,下一步移动到的格子为 $(xx,yy)$,那么:
1. 当 $(x,y)$ 和 $(xx,yy)$ 之间没有墙时,你可以直接移动到 $(xx,yy)$,整个过程算 $1$ 步。
1. 当 $(x,y)$ 和 $(xx,yy)$ 之间有墙时,那么你可以把这堵墙往 $dir$ 方向推一格,但要保证推到的地方没有墙且在网格图内(含边界),然后再走到 $(xx,yy)$,整个过程算 $1$ 步。
最后问你当你离开网格图(走出边界)的步数最少时,这条路径是什么。**(注意:走出边界的那一步也算入总步数)**
输入格式
输入包含多组数据,以 ```0 0``` 结束输入。
第 $1$ 行给出两个数 $x$ 和 $y$ 为起点的坐标。
第 $2\sim 5$ 行,每行有 $6$ 个数。第 $i+1$ 行的第 $j$ 个数代表网格图中 $(i,j)$ 的权值。
输出格式
输出一行字符串,描述从起点走出网格图的最短路径。其中东西南北分别用'E'、'W'、'S'、'N'表示。
### 样例解释:
一开始:

向上推墙:
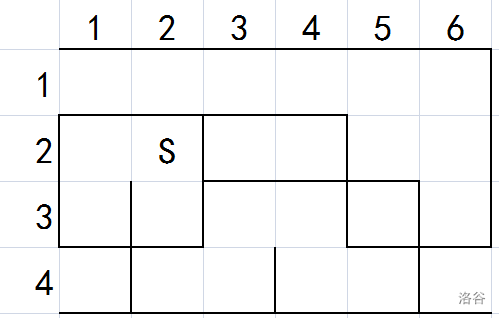
向右推墙:
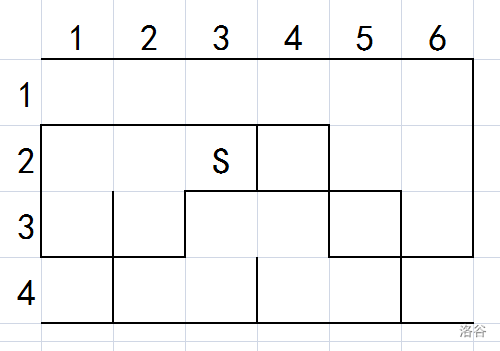
向下推墙:
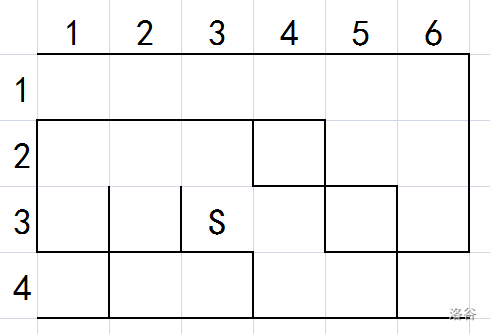
沿着空格子走:
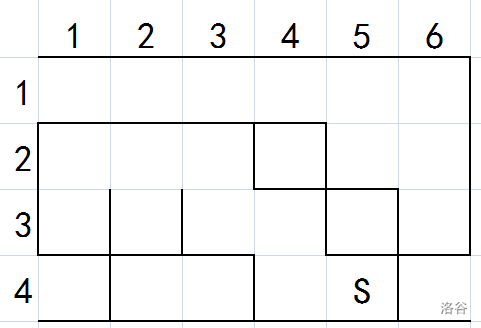
向右推墙:

向上推墙($2$ 步):
直接走到终点:(路线也标出来了)

然后按东南西北大写缩写的方式输出路线:
$NESESEENNWNWWWWW$