UVA10572 Black & White
题目描述
题目大意
一个m×n的网格，有的格子已经染上黑色或白色，现在要求将所有的未染色格子染上黑色或白色，使得满足以下2个限制：
1) 所有的黑色的格子是四连通的，所有的白色格子也是四连通的。
2) 不会有一个2×2的子矩阵的4个格子的颜色全部相同。
如图1，3不合法，图2，4合法。
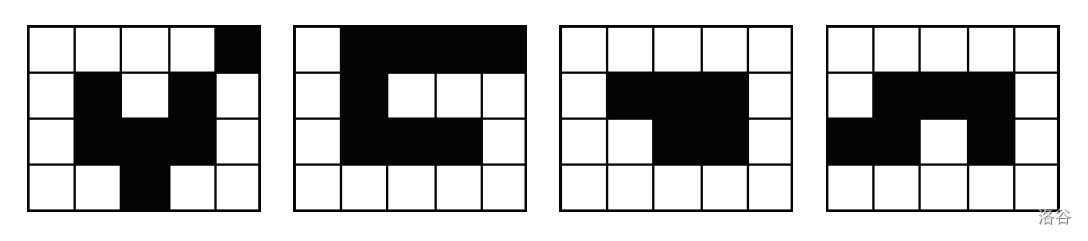
求方案总数和其中一组方案。(m, n ≤ 8)
输入格式
无
输出格式
无