UVA1091 Barcodes
题目描述
## 题目背景
code-11 是一种条形码编码系统,用来将一个字符串编码为条形码。
在这种编码系统中,可以使用的字符仅有数字 $0$ 到 $9$ 以及 $-$ 号,以及特殊的 start/stop 字符放在条形码的开头和结尾。
对于每个字符,都对应了一个长度为 5 的 01 串。如下所示。
|字符|编码|
| :----------- | :----------- |
|$0$|00001|
|$1$|10001|
|$2$|01001|
|$3$|11000|
|$4$|00101|
|$5$|10100|
|$6$|01100|
|$7$|00011|
|$8$|10010|
|$9$|10000|
|$-$|00100|
|start/stop|00110|
对应到条形码中,每个条形码都是由黑白相隔的条带组成的,且第一个条带为黑色。条带分为宽和窄两种,宽带的宽度为窄带的两倍,`0` 表示窄的条带,$1$ 表示宽的条带。而每两个相邻的字符之间一定是一个白色窄带作为分隔。
举个例子,字符 $1$:
`10001` 表示粗细细细粗,然后因为黑白要间隔,所以就是 黑粗 白细 黑细 白细 黑粗,如下图所示:
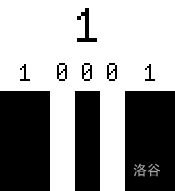
为了能够检测条形码的正确性,我们加入两个检测数字 $C$ 和 $K$,加在条形码的末尾(在 stop 之前)。
设需编码的字符串为 $c_1c_2\dots c_n$,则:
$C=\left(\sum\limits_{i=1}^n((n-i)\bmod10+1)\cdot w(c_i)\right)\bmod11$
$K=\left(\sum\limits_{i=1}^{n+1}((n-i+1)\bmod9+1)\cdot w(c_i)\right)\bmod11$
这里 $c_{n+1}=C$,且 $w(c)$ 表示 $c$ 的权重,如果 $c$ 是 $0$ 到 $9$ 中的一个,那么对应的权重就是 $c$,`-` 的权重为 10。
举个例子,对于字符串 `123-45`:
|计算过程|$c_1$|$c_2$|$c_3$|$c_4$|$c_5$|$c_6$|$c_7$|$c_8$|
| -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: |
|字符|$1$|$2$|$3$|$-$|$4$|$5$|||
|每个字符的权值|$1$|$2$|$3$|$10$|$4$|$5$|||
|$((n-i)\bmod10)+1$|$6$|$5$|$4$|$3$|$2$|$1$|||
|乘起来求和,$C=$|$1\times6+$|$2\times5+$|$3\times4+$|$10\times3+$|$4\times2+$|$5\times1=$|$71\bmod11=5$||
|字符|$1$|$2$|$3$|$-$|$4$|$5$|$5$||
|每个字符的权值|$1$|$2$|$3$|$10$|$4$|$5$|$5$||
|$((n+1-i)\bmod10)+1$|$7$|$6$|$5$|$4$|$3$|$2$|$1$||
|乘起来求和,$K=$|$1\times7+$|$2\times6+$|$3\times5+$|$10\times4+$|$4\times3$|$5\times2+$|$5\times1=$|$101\bmod11=2$|
|最终结果|$1$|$2$|$3$|$-$|$4$|$5$|$5$|$2$|
所以,结果就是 $123-4552$,并在前后加上 start 和 stop 符号。
在实际应用中,通过探测器探测出每个条带的宽度后,通过解析软件将条形码还原为原本的字符串。
由于条形码方向并未固定,所以软件必须自己判断这个条形码是从左至右的还是从右至左的。现在,你的任务是扫描并解析一个条形码。你所拥有的信息为每个条带的宽度,但由于设备总是会有误差的,所以,宽带宽度不一定严格的是窄带的宽度的两倍,你的程序需要能够容忍 5% 的误差。
输入格式
本题有多组数据。
输入第一行包括一个整数 $T$,表示测试数据的组数。
对于每组数据首先是一个整数 $n$ 表示该条形码有多少条带。接着 $n$ 个整数 $d_1,d_2,\dots,d_n$ 以空格隔开表示了每个条带的宽度。再次强调你并不知道这个条形码是从左至右的还是从右至左的,你需要正着和反着都判断一遍。
输出格式
对于每组数据输出一行。输出时分如下几种情况。若该条形码合法,则输出解析所得的原字符串,不包括检测字符 $C$ 和 $K$。若可以成功解析但是检测字符 $C$ 错了,则输出 `bad C`。若 $C$ 也是对的,但 $K$ 是错的,则输出 `bad K`。对于剩下所有情况输出 `bad code`。
说明/提示
> 注意A相对于B误差