UVA11864 Probability Calculation

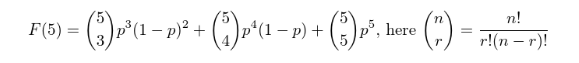
在客机生产领域，波音和空客是两个最主要的生产商。波音制造的飞机有两个引擎而空客有四个。但这并不说明空客飞机比波音的飞机安全。波音和空客都在尝试尽可能的提升他们的产品，但这并不会解决这个问题。 关于双发客机和四发客机，这里有一些有趣的事实。很多人说，为了使一架客机安全的停留在空中，至少$50$%的引擎必须可以工作。在这道题（UVA11864）中，我们假设之句话是正确的。所以，如果有一架飞机有$5$个引擎，则为了完成一次安全的飞行必须至少有$3$个引擎可以工作。如果所有引擎都有相等的概率$p$维持工作但是故障又不相同时，我们可以用二项式定理(binomial theorem)来计算完成一次飞行的概率。例如，一架有$5$个引擎的客机，完成一次飞行的概率就是  所以， 另外定义函数$CF$: 现在的飞机已经很少见到多于$4$个引擎的飞机了。不过科学家们正在计划制造一种有着成千上万的小型引擎的飞机。原因如下： 1. 上文的概率算出的结果仅在物品数量十分大时才与现实生活对应。例如抛硬币时正面向上的概率为$0.5$。但在现实生活中，扔十次不一定就会有5次正面向上。但如果我们抛$10000$次，那向上的次数就有$5000$次左右。 2. 通常情况下，造一个不会出错的引擎比造出一个$p$（例如$0.6$）非常低的引擎要贵的多。所以如果一架飞机有$10000$个引擎，在现实生活中，$50$%的引擎都不能正常工作的概率很低即使$p$是$0.6$左右。 这个问题（UVA11864）中，你的任务就是帮助科学家在给定$m$和$p$的情况下找到$CF$函数的值。科学家们说这些值对于他们的研究十分有用。

输入的文件包含约$12$组数据。下面是每一组数据的描述： 第一行包含一个浮点数$p$($0 \leq p\leq1$)和一个整数$Q$($0 \leq Q \leq 2000$) 这里$p$指引擎**不会**故障的概率，$Q$指询问的总数。 接下来$Q$行，每行一个整数$m$($0 \leq m \leq 50001$)。 当$Q$为$0$时输入结束。

对于每组$Q+1$行的输入。第一行应当包含连续的组数（序号）。接下来$Q$行应当包含一个浮点数，也就是函数$CF(m)$的值。这些浮点数应当保留8位小数。误差允许最大范围 您还可以查看样例的输出细节。