UVA1214 Manhattan Wiring

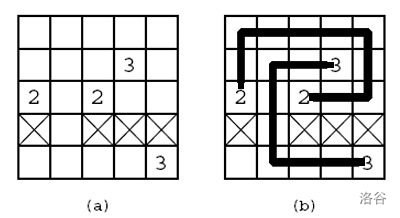
在一个 $N \times M$ 的网格里有空格和障碍，其中两个空格子里标记着 $2$，还有两个空格子标记着 $3$。 你的任务是把这两个 $2$ 和两个 $3$ 在限制条件下各用一条折线连起来，使得总长度尽量小（线必须穿过格子中心，每个单位正方形的边长为 $1$）。 限制条件如下：障碍格里不能有线，而每个空格里最多只能有一条线。由此可知，两条折线不能相交，每条折线不能自交。 如图所示，折线总长度为 $18$。 **请注意，四个作为起点和终点的 $2$、$3$ 格子内各有一小节长度为 $0.5$ 的线。不要忘了它们。** 

输入包含多组数据。每组数据的第一行为两个正整数 $N$ 和 $M$（$1 \le N,M \le 9$），以下 $N$ 行每行为 $M$ 个整数，来描述该网格。`0` 表示空格，`1` 表示障碍，`2` 表示写有 $2$ 的格子，`3`表示写有 $3$ 的格子。 输入终止标记为 `0 0`。

对于每组数据输出一行，输出两条折线最小总长度。如果无解，输出 `0`。

本题较为卡常。