A Scheduling Problem

感谢 佚名 提供翻译，感谢 @皎月半洒花 完善了翻译。

[problemUrl]: https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=446&page=show_problem&problem=4126 [PDF](https://uva.onlinejudge.org/external/13/p1380.pdf) 现有一些需要安排的任务 $x_1, x_2, …, x_n$。每个任务需要一天来完成。你的任务是给这些任务调度，使得能用最少的天数完成它们。不同任务之间有两种约束条件： _**相互冲突**_ 以及 _**优先关系**_ 。 1、相互冲突：两个任务不能在同一天内完成。(可能是因为任务 $x_i$ 与任务 $x_j$ 需要使用同一个机器，所以它们必须在不同的日期完成) 2、优先关系：对于两个任务，其中的一个任务需要在另一个任务开始之前完成。(比如说，某一个任务 $x_i$ 在某一个任务 $x_j$ 完成之前，是不能开始的) 你的任务安排需要满足所有的约束条件。 为了记录下各个约束条件，我们构造了以任务 $x_1, x_2, …, x_n$ 为节点的图 $\rm G$。假如 $x_i$ 与 $x_j$ 不能在同一天完成，就在 $x_i$ 与 $x_j$ 之间连一条无向边。假如 $x_i$ 需要在 $x_j$ 之前完成，就在 $x_i$ 与 $x_j$ 之间连一条从 $x_i$ 指向 $x_j$ 的有向边。 当然，假如构造出的图十分复杂，这个调度问题就会十分困难。因此我们假定，在我们的问题中，各个约束条件并没有那么复杂：我们需要考虑的图 $\rm G$，总是成一个树形结构（在忽略边的方向性之后）。你的任务就是去求出最佳调度方案所需的天数。你可以使用这个定理： >假如 $\rm G$ 是一棵树，那么需要的天数是 $k$ 或 $k+1$ 。$k$ 满足：$k$ 是 $\rm G$ 中所有链中一条链能包含的最多顶点数。 > >链的定义：在一条路径 $ P=(x_1, x_2, …, x_k)$中 ，对于任意的 $i=1,2,…,k-1$，总有一条从 $x_i$ 指向 $x_{i+1}$ 的有向边。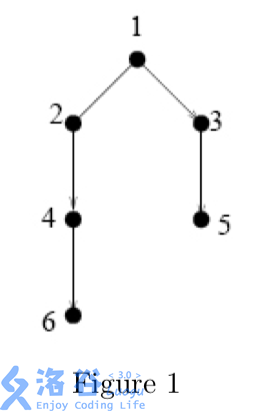  图一就是一个样例。有六个任务：$1,2,3,4,5,6$。从这张图中，我们可以看出，任务 $1$ 与任务 $2$ 必须在不同日期完成。任务 $1$ 需要在任务 $3$ 之前完成，任务 $3$ 需要在任务 $5$ 之前完成，任务 $2$ 需要在任务 $4$ 之前完成，任务 $4$ 需要在任务 $6$ 之前完成。不难看出，完成所有任务所需的最小天数是 $4$ 天。在这个样例中，一个链所包含的最大顶点数 $k$ 就是 $3$ 。

输入包含一些树（边可能为有向边或无向边）的数据$T_1,T_2,…,T_m,m<=20$。每棵树上至多有$200$个结点。我们用有根树来代表某一棵树（这只是为了表示树时能方便一些，并且“根”是随机选取的点）。每棵树的信息包含几行数据：每一行的第一个数字（正整数）是某一个顶点的编号，随后的数字是他的儿子节点（也是正整数），在一行的最后以一个$0$结束。需要注意的是，$0$并不是一个顶点的编号，仅代表该行数据已经结束。 当然，有一些边是有向边。有向边的方向可以是从父节点指向子节点，也可以是从子节点指向父节点。如果这条边是从父节点指向子节点的，那么我们在子节点编号之后标上字母 $d$ (意思是downward edge)；如果这条边是从子节点指向父节点的，那么我们在子节点编号后标上字母 $u$ (意思是upward edge)；如果这条边是无向边，那么我们在子节点编号后不放置任何字母。 输入样例的第一组数据就是图一样例。 每一行的节点编号（其后有字母时，包括该字母）用一个空格隔开。假如某一行数据仅有一个数字 $0$，则代表这棵树的数据已输入完毕。下一棵树的数据从它的下一行开始输入。连续两行的 $0$ 代表所有输入已结束。

每一组数据的输出独占一行。每行仅有一个数字，即完成数据对应的调度问题所需的最小天数。

1 2 3d 0
2 4d 0
3 5d 0
4 6d 0
0 
1 2d 3u 4 0 
0
1 2d 3 0
2 4d 5d 10 0 
3 6d 7d 11 0 
6 8d 9 12 0 
0
1 2 3 4 0
2 5d 0
3 6d 0
4 7d 0
5 8d 0
6 9d 0
7 10d 0
0
0 

4
3
4
3