UVA1543 圆和多边形 Telescope

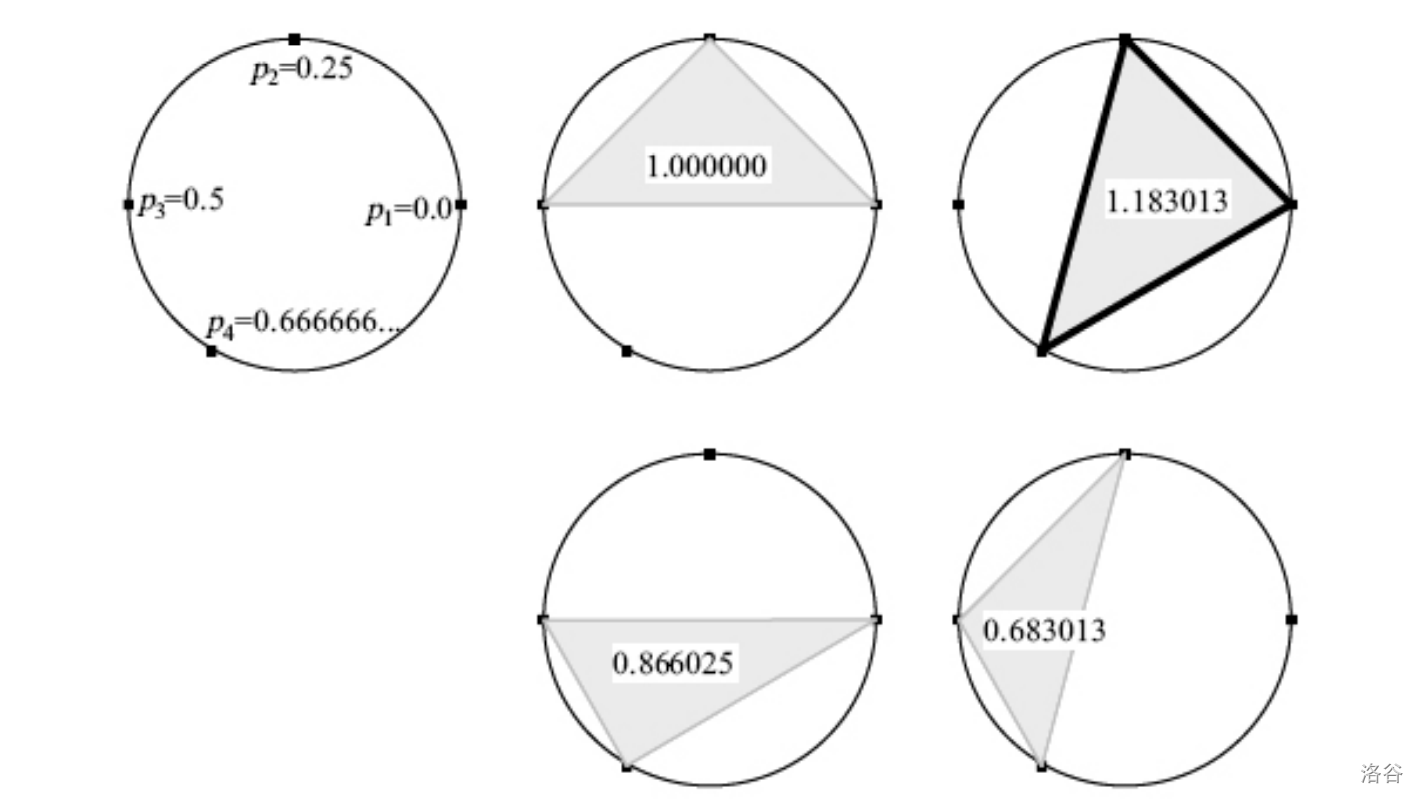
极限博士建造了一台高度精准的望远镜，他想通过这台望远镜对遥远的奇异天象进行观测。为了使其足够精准以保证观测效果，极微小的扰动失真都是不容许的。虽然博士非常细心，但百密一疏，他忘记了望远镜内部空气的影响。空气会被穿过望远镜的低频磁场流影响而产生扰动失真，但望远镜的筒壁不受影响。 望远镜镜筒的横截面是一个完美的圆，为了测量磁场流的强度，极限博士想在内圆周布上极细的导线，这些导线形成的线圈可以帮助博士测量并估计磁场带来的影响。但是，圆周上能固定导线的点只有 $n$ 个，而能固定导线的特殊夹子个数只有 $m$ 个。为了实现线圈的最高灵敏度，博士想让固定在圆周上的导线形成的多边形面积最大。请你帮助他找出这个最大的多边形。圆的半径为 $1$。 图中所示的是 $n = 4, m = 3$ 时的所有可能的多边形，多边形中的数表示面积大小，$p_i$ 表示给定点 $i$ 与标准原点 $0$ 之间的圆弧长度与圆周长的比值。（图片来源：原 [PDF](https://onlinejudge.org/external/15/p1543.pdf)） 

对于每一个子问题，第一行为两个整数 $n, m$。 接下来一行有 $n$ 个递增的实数，表示圆周上固定点的位置，实数的含义是点与标准原点 $0$ 之间的圆弧长度与圆周长的比值。（随着实数增大，默认点逆时针分布）所有实数均不小于 $0$ 且均小于 $1$。 输入以 `0 0` 结束。

问题由多个子问题构成。 对于每一个子问题，输出一个实数，表示最大的多边形面积，保留 $6$ 位小数，误差须小于 $10^{-6}$。 子问题之间输出须分行。

### 数据范围 对于所有数据，$3 \le m \le n \le 40$。