UVA1686 平铺 Tiling

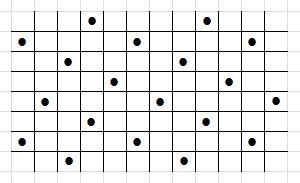
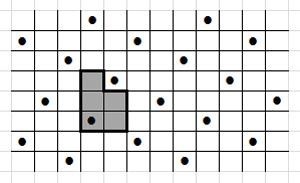
分析地板的图案是一件很有意思的事情，尤其是观察那种地砖上有不同图案的地面。 现在假设在一个无限大的广场地面上，有无数个大小相同的正方形地砖，这些地砖有两种类型：有点和空白（如图）  显然这样的地砖看上去可以被分成很多完全相等的小块（大小，形状，内部图案均相等）（如图）  同时我们发现，我们可以无缝的用上述小块覆盖住整个广场（如图）  现在我们所需要解决的问题，就是在一个无穷大的、给出点的位置规律的广场上找出最小的分块方案。 点的规律的给出方式很特别： 给出dx1,dx2,dx3及dy1,dy2,dy3使得所有的点的位置满足 $x= dx1\ast i+dx2\ast j+dx3\ast k$ $y= dy1\ast i+dy2\ast j+dy3\ast k$ 其中i,j,k为整数 而其他的砖块就是空白的。

第一行1个正整数T，表示数据组数 第2 - T+1行 6个正整数，分别表示dx1,dy1,dx2,dy2,dx3,dy3(保证三个参数所给出的点不同)

对于第i个询问，输出Case#i: num （此处num表示该情况下最小的分块面积）

保证$1\leqslant T\leqslant 1000$ 保证所有数据都在长整型范围内