欧拉路径
题单介绍
# 欧拉路径
> 注意区分“回路”和“路径”
## 存在性
#### 无向图
所有点的度数均为偶数,或有且仅有两个度数为奇数的点
#### 有向图
##### $\colorbox{blue}{\color{white}{注意,定义与无向图不可混淆,与单纯的入度/出度奇偶性无关}}$
所有的点入度等于出度,或者:有且仅有一个点入度-出度=1,同时有且仅有一个点出度-入度=1
##### $\color{red}{当心不连通!}$
## 求法
> 用**DFS搜索**思想求解欧拉回路的思路为:利用欧拉定理判断出一个图存在欧拉通路或回路后,选择一个正确的起始顶点,用DFS 算法遍历所有的**边**(每条边**只遍历一次**),遇到走不通就**回退**。在搜索前进方向上将遍历过的**边**按顺序记录下来。这组边的排列就组成了一条欧拉通路或回路。
>
> ——转载自[这里](https://blog.csdn.net/u011466175/article/details/18861415)及其它相关内容
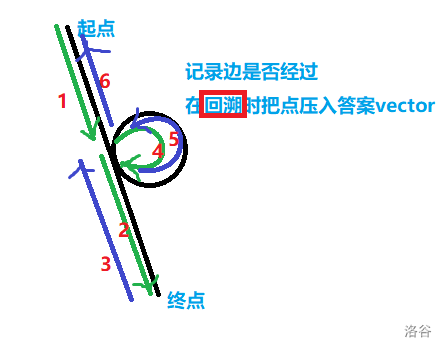
P.S. 同时用 $vis$ 数组记录**边**;无向图的边在记录时要同时删一对
```cpp
void dfs(int u) {
for(unsigned i = edge[u]; i < e[u].size(); i = max(i + 1, (unsigned)edge[u]) /* 巧妙之处,动态删边 */ ) {
int v = e[u][i].first, id = e[u][i].second;
if(st[id]) continue;
st[id] = 1;
edge[u] = i + 1;
dfs(v);
}
tt ++ ; ans[tt] = u;
}
```