【硬核】集合论 - 序数 - 第十一章 - 1-Y
Butterfly_qwq
·
·
算法·理论
这是这一系列的第十一章,第十章在这。
上面的 BMS 扩展虽然规则看起来强大,但是实际强度却不尽如人意甚至有可能强度和 BMS 一样。
另外还有一个东西叫做 TBMS,他把 BMS 扩展到了 \Omega 维、甚至 \omega_1(第一个不可数序数) 维的结构。Bubby3 把它扩展到更加高的结构。
但是,接下来介绍的 1-Y 甚至只用了 \omega+1 维就薄纱各种 TBMS。
除了 Bubby3's TBMS Extended,没有任何 TBMS 能过 Y(1,3,4,3) 这个提升(注意,由于 1-Y 比 0-Y 出现要早,所以一般的 Y 都是指的 1-Y 而不是 0-Y)。
有以下分析:
神奇,上一秒还是不是很大的 $\omega^\omega$,下一秒直接到递归序数极限了。
将最后一个数改成 $11$ 更是直接薄纱所有 TBMS(除了 Bubby3 的,那个挺牛),作为对比,$Y(1,3,4,2,5,8,10,4,9,14,17,10)=(0,1^{\omega_1})=\aleph\text{SSO}$。
然后,用 Bubby3's TBMS 可以得到 $Y(1,3,4,3)=(0)(1^{2,1^3})$。
Bubby3's TBMS 的极限是 $Y(1,3,7,14)$,仍然没有达到 $Y$ 极限的一点点影子。
说了这么多……
你 TM 赶紧说 Y 序列是啥啊!
---
先讲一讲 Y 的山脉图怎么画吧。
先按 0-Y 规则做出山脉图,不过这里有一点不一样——如果一个元素是 $1$,那么山脉图在它顶上的元素不是 $1$ 而是“空”,然后如果按着 0-Y 规则找不到父项了就是没有父项,不用管它。
比如说 $Y(1,2,4,5,7)$ 的山脉图就是:
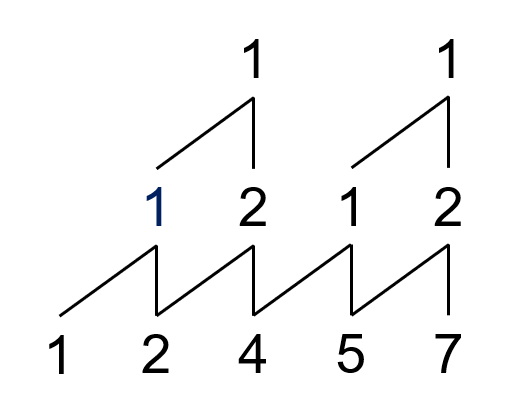
但是如果画完山脉图之后,存在一列顶点元素不是 $1$ 该怎么办?
比如说,$Y(1,3)$?
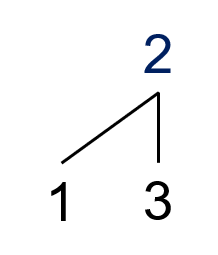
我们可以把所有顶点元素组成一个新序列,此时找父项要到提取前的序列去找。
比如说,$Y(1,3,7,14,7,13)$。
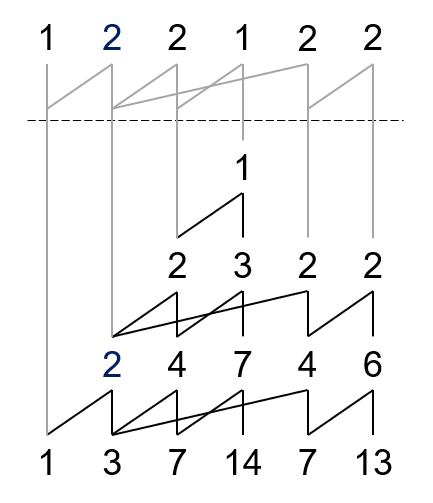
然后再根据规则做一下山脉图就好了。
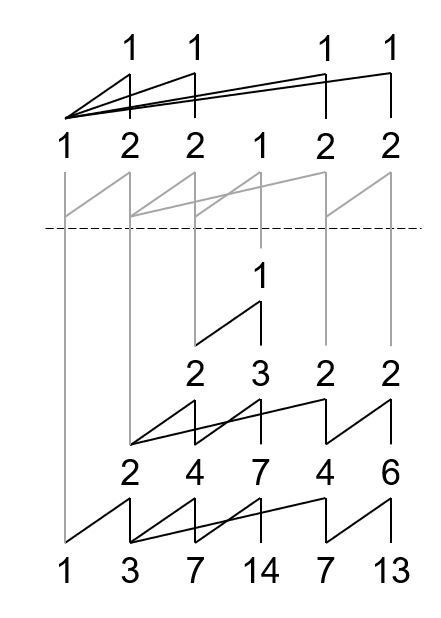
当然,也有可能提取两次,比如说 $Y(1,4,11,21)$。
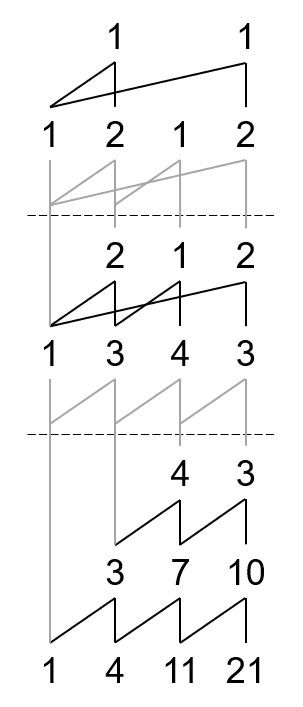
这便是 1-Y 山脉图的画法了。
---
然后就是 1-Y 的展开。
父项定义和 0-Y 有些许不同,是元素向下沿着左边走,然后再往正上方走,**不能跨线,如果后一步无法实现就不实现**,其他定义一样。
在 0-Y 中没有加粗部分,因为后一步总能实现。
最上层 0-Y 规则。
从次上层开始,事情变得不太一样。
我们还是先定义几个概念。
顶点元素:从根元素起,重复“先向右上走一步再向正下走 0~1 步”所能达到每一列的最高点。
轮廓边:从任意顶点元素起,重复“先向右上走一步再向正下走一步”直到走不了可能经过的所有边。
平移边:根列右侧不是轮廓边就是平移边。
参考边:从根元素起,重复“先向右上走一步再向正下走一步”直到走不了可能经过的所有边。
次上层,包括除最上层外的所有层的展开规则其实就三句话:提升轮廓边,平移平移边,填充参考边。
1. 提升轮廓边:两条横线间的山脉图高度的定义为最右列顶点元素和根元素的高度之差。每次将轮廓边除了平移宽度以外还要提升高度,每次提升的高度就是山脉图的高度;
2. 平移平移边:对于所有平移边,直接平移。
3. 填充参考边:注意到轮廓边和平移边之间会产生一些空隙,这些空隙用参考边进行所需填充。
其实还是可以理解。
举个经典例子:
$Y$ 的巨大提升:$Y(1,3,4,3)$。
先画出山脉图,然后展开上层,标注下层:
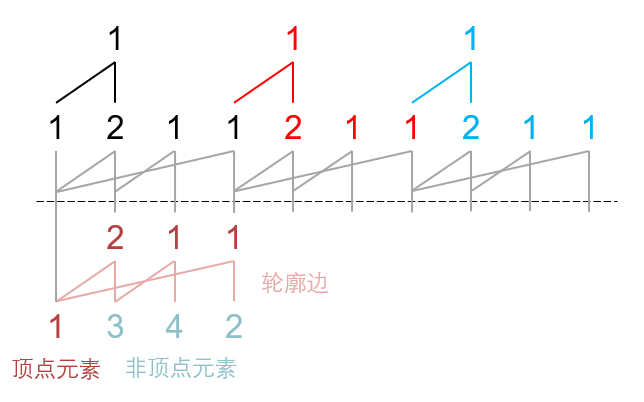
提升轮廓边,平移平移边(这里没有平移边):
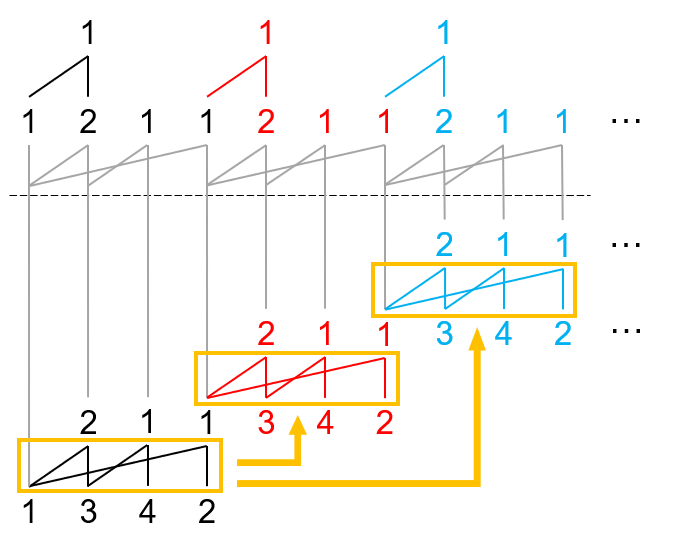
右下出现了一定的空隙,用参考边(这个例子中和轮廓边一样)填充:
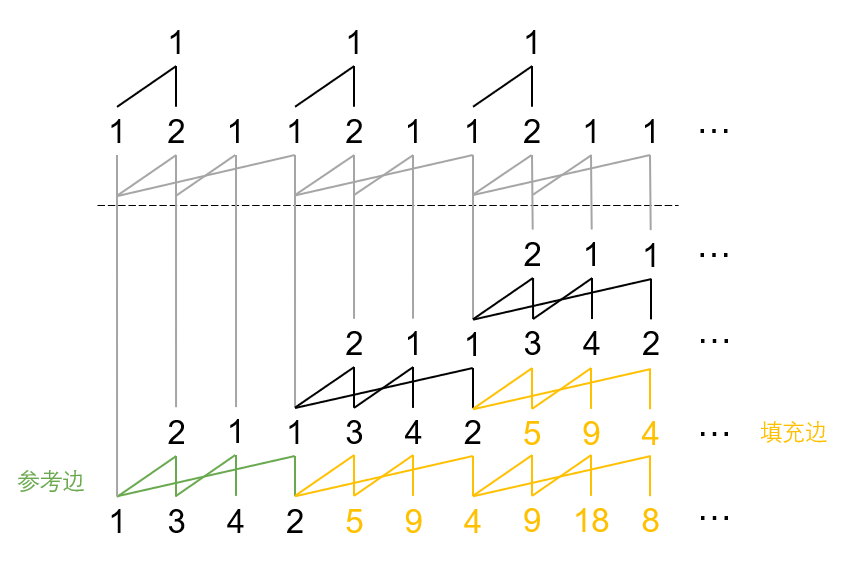
大功告成,$Y(1,3,4,3)=Y(1,3,4,2,5,9,4,9,18,8,\dots)$。
更多的例子没有必要,~~我不在狸那里贺更多的图了~~,相信大家都已经理解了。
---
Y 的扽西是困难的,因为它和 BMS 差了很多。
接下来我们将会使用序数行 BMS 来扽西,目标是 $Y(1,3,4,2,5,8,10)$。
单行 BMS(PrSS)就是 Y,跳过。重要节点标绿,极其重要节点标红。
$$\color{red}BM(0)(1,1)=Y(1,2,4)$$
$$BM(0)(1,1)(0)(1,1)=Y(1,2,4,1,2,4)$$
$$BM(0)(1,1)(1)=Y(1,2,4,2)$$
$$BM(0)(1,1)(1)(2,1)(2)=Y(1,2,4,3)$$
$$BM(0)(1,1)(1,1)=Y(1,2,4,4)$$
$$BM(0)(1,1)(2)=Y(1,2,4,5)$$
$$BM(0)(1,1)(2,1)=Y(1,2,4,6)$$
$$\color{green}BM(0)(1,1)(2,2)=Y(1,2,4,7)$$
$$BM(0)(1,1)(2,2)(1,1)=Y(1,2,4,7,4)$$
$$BM(0)(1,1)(2,2)(2)=Y(1,2,4,7,5)$$
$$BM(0)(1,1)(2,2)(2,1)=Y(1,2,4,7,6)$$
$$BM(0)(1,1)(2,2)(2,1)=Y(1,2,4,7,7)$$
$$BM(0)(1,1)(2,2)(3)=Y(1,2,4,7,8)$$
$$BM(0)(1,1)(2,2)(3,1)=Y(1,2,4,7,9)$$
$$BM(0)(1,1)(2,2)(3,2)=Y(1,2,4,7,10)$$
$$\color{green}BM(0)(1,1)(2,2)(3,3)=Y(1,2,4,7,11)$$
$$BM(0)(1,1)(2,2)(3,3)(4,4)=Y(1,2,4,7,11,16)$$
$$\color{red}BM(0)(1,1,1)=Y(1,2,4,8)$$
$$BM(0)(1,1,1)(1)=Y(1,2,4,8,2)$$
$$BM(0)(1,1,1)(1)(2,1,1)(2)=Y(1,2,4,8,3)$$
$$BM(0)(1,1,1)(1,1)=Y(1,2,4,8,4)$$
$$BM(0)(1,1,1)(1,1)(2,2,1)(2)=Y(1,2,4,8,5)$$
$$BM(0)(1,1,1)(1,1)(2,2,1)(2,1)=Y(1,2,4,8,6)$$
$$BM(0)(1,1,1)(1,1)(2,2,1)(2,2)=Y(1,2,4,8,7)$$
$$BM(0)(1,1,1)(1,1,1)=Y(1,2,4,8,8)$$
$$BM(0)(1,1,1)(2)=Y(1,2,4,8,9)$$
$$BM(0)(1,1,1)(2,1)=Y(1,2,4,8,10)$$
$$BM(0)(1,1,1)(2,1)(1,1)(2,2,1)(3,2)=Y(1,2,4,8,11)$$
$$BM(0)(1,1,1)(2,1,1)=Y(1,2,4,8,12)$$
$$BM(0)(1,1,1)(2,2)=Y(1,2,4,8,13)$$
$$BM(0)(1,1,1)(2,2,1)=Y(1,2,4,8,14)$$
$$\color{green}BM(0)(1,1,1)(2,2,2)=Y(1,2,4,8,15)$$
$$BM(0)(1,1,1)(2,2,2)(3,3,3)=Y(1,2,4,8,15,26)$$
$$\color{red}BM(0)(1,1,1,1)=Y(1,2,4,8,16)$$
$$BM(0)(1,1,1,1)(2,2,2,2)=Y(1,2,4,8,16,31)$$
$$BM(0)(1,1,1,1,1)=Y(1,2,4,8,16,32)$$
$$BM(0)(1,1,1,1,1,1)=Y(1,2,4,8,16,32,64)$$
$$\color{red}BM(0)(1^\omega)=Y(1,3)$$
至此达到了普通 BMS 的极限,往后我就仅仅给几个节点,不作详尽的分析了(4.5k 字)。
$$BM(0)(1^\omega)(2,1^\omega)=Y(1,3,4,2,5,7,5)$$
$$BM(0)(1^\omega)(2,2)=Y(1,3,4,2,5,7,10)$$
$$\color{green}BM(0)(1^\omega)(2^\omega)=Y(1,3,4,2,5,7,10,5)$$
$$\color{red}BM(0)(1^{\omega+1})=Y(1,3,4,2,5,7,11)$$
$$BM(0)(1^{\omega+1})(2^{\omega+1})=Y(1,3,4,2,5,7,11,18)$$
$$\color{green}BM(0)(1^{\omega+2})=Y(1,3,4,2,5,7,11,19)$$
$$BM(0)(1^{\omega+3})=Y(1,3,4,2,5,7,11,19,35)$$
$$\color{red}BM(0)(1^{\omega2})=Y(1,3,4,2,5,7,12)$$
$$\color{green}BM(0)(1^{\omega3})=Y(1,3,4,2,5,7,12,16,25)$$
$$BM(0)(1^{\omega4})=Y(1,3,4,2,5,7,12,16,25,33,50)$$
$$\color{red}BM(0)(1^{\omega^2})=Y(1,3,4,2,5,8)$$
$$\color{green}BM(0)(1^{\omega^3})=Y(1,3,4,2,5,8,8)$$
$$BM(0)(1^{\omega^4})=Y(1,3,4,2,5,8,8,8)$$
$$\color{green}BM(0)(1^{\omega^\omega})=Y(1,3,4,2,5,8,9)$$
$$BM(0)(1^{(0)(1)(2)})=Y(1,3,4,2,5,8,9,10)$$
$$\color{green}BM(0)(1^{(0)(1,1)})=Y(1,3,4,2,5,8,9,11)$$
$$BM(0)(1^{(0)(1,1,1)})=Y(1,3,4,2,5,8,9,11,15)$$
$$BM(0)(1^{(0)(1^\omega)})=Y(1,3,4,2,5,8,9,12)$$
$$BM(0)(1^{(0)(1^{(0)(1^\omega)})})=Y(1,3,4,2,5,8,9,12,15,16,19)$$
$$\color{red}BM(0)(1^\Omega)=Y(1,3,4,2,5,8,10)$$
至此,BMS 的分析达到了极限,往后已经几乎没有记号可以分析它了。
我们令 $SYO=Y(1,\omega)$,但是我们不知道它有什么性质。
哦对了值得一提的是:
接下来要说的 ω-Y 极限是 MHO,但是还没有 LHO 和 MYO。所以如果你的符号定义强度极高并且是 worm 型,那么大数界一般说这个符号拥有“LHO 定义权”或“MYO 定义权”。
1-Y 完。