【硬核】集合论 - 序数 - 第九章 - lPrSS&hPrSS&0-Y
Butterfly_qwq
·
·
算法·理论
这是这一系列的第九章,第八章在这。
我们回到了对 PrSS 的扩展。我们会讲的是 lPrSS。
说来 lPrSS 也简单,就是去除 PrSS 中 a_i+1\ge a_{i+1} 的性质,定义展开方式如下:
-
- 若 a_n=1,则把 a_n 删去计算序数,再把计算完的结果 +1;
- 如果 a_n\not=1,则把好部保留,把最后一个数删去,把坏部无限重复,并且每次重复都是上一次重复的值加上 a_n-a_k-1,其中 a_k 是坏根,例如 (1,2) 展开成 (1,1,1,1,\dots),(1,2,3) 展开成 (1,2,2,2,2,\dots),(1,3,3) 展开成 (1,3,2,4,3,5,4,6,\dots)。
那么继续开始扽西。
写了几个关键点,事实上分析起来还是很构式的。
$(1,3)=\varepsilon_0,(1,3,1,3)=\varepsilon_02,(1,3,2)=\varepsilon_0\omega,(1,3,2,2)=\varepsilon_0\omega^2,(1,3,2,3)=\varepsilon_0\omega^\omega,(1,3,2,3,4)=\varepsilon_0\omega^{\omega^\omega},(1,3,2,4)=\varepsilon_0^2,(1,3,2,4,2,4)=\varepsilon_0^3,(1,3,2,4,3)=\varepsilon_0^\omega,(1,3,2,4,3,3)=\varepsilon_0^{\omega^2},(1,3,2,4,3,4)=\varepsilon_0^{\omega^\omega},(1,3,2,4,3,4,5)=\varepsilon_0^{\omega^{\omega^\omega}},(1,3,2,4,3,5)=\varepsilon_0^{\varepsilon_0},(1,3,3)=\varepsilon_1,(1,3,3,3)=\varepsilon_2,(1,3,4)=\varepsilon_\omega,(1,3,4,4)=\varepsilon_{\omega^2},(1,3,4,5)=\varepsilon_{\omega^\omega},(1,3,5)=\varepsilon_{\varepsilon_0},(1,4)=\zeta_0$。
从 $1,4$ 到 $1,5$ 是春春答辩,有兴趣的各位可以品尝一下,这里就不过多说明了。
$(1,4,2)=\zeta_0\omega,(1,4,2,4)=\zeta_0\varepsilon_0,(1,4,2,5)=\zeta_0^2,(1,4,2,5,3)=\zeta_0^\omega,(1,4,2,5,3,5)=\zeta_0^{\varepsilon_0},(1,4,2,5,3,6)=\zeta_0^{\zeta_0},(1,4,3)=\varepsilon_{\zeta_0+1},(1,4,4)=\zeta_1,(1,4,4,4)=\zeta_2,(1,4,5)=\zeta_\omega,(1,4,6)=\zeta_{\varepsilon_0},(1,4,7)=\zeta_{\zeta_0},(1,5)=\eta_0$。
$(1,5,2)=\eta_0\omega,(1,5,3)=\varepsilon_{\eta_0+1},(1,5,4)=\zeta_{\eta_0+1},(1,5,5)=\eta_1,(1,5,6)=\eta_\omega,(1,5,7)=\eta_{\varepsilon_0},(1,5,8)=\eta_{\zeta_0},(1,5,9)=\eta_{\eta_0},(1,6)=\vartheta_0,(1,7)=\iota_0,\dots,(1,\omega)=\varphi(\omega,0)$。
lPrSS 的规则是简单的,与之相对的是,它的极限也是弱的。
---
接下来到场的是 hPrSS。与 lPrSS 不同,hPrSS 充分运用了“阶差”的思想。
定义在序列中一个数的“子坏根” $c_i$ 为 $\max\{k<i|a_k<a_i\}$,“阶差” $b_i$ 为 $a_i-a_{c_i}$。
展开时,如果最后一项阶差为 $1$ 则按 PrSS 规则展开。
否则,画出山脉图。
山脉图绘画方式如下:
在 $a_i$ 上方写上数字 $b_i$,并连两条线,一条是从 $a_i$ 连到 $b_i$,一条是从 $a_{c_i}$ 连到 $b_i$。
这时候,上方的一个数的父项为:向左下走一步再向上走一步,一直重复直到得到一个小于当前数的数为止。
举个例子:$(1,4,6,4,1,4,6,3,6,8)^H$。
画出山脉图是(感谢知乎用户 Suzuka梅天狸 提供的图片,以后类似风格的图都是从他那里贺的):
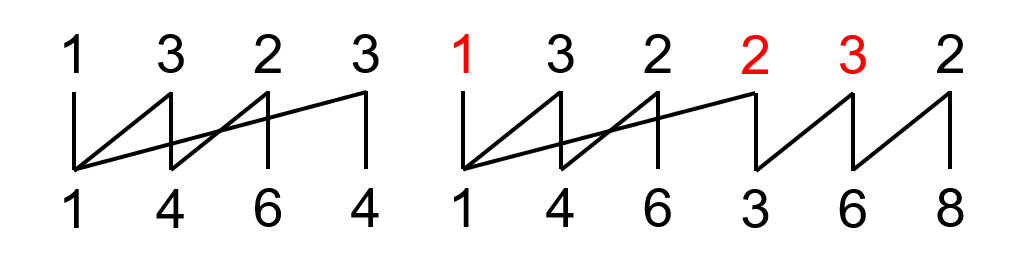
那么右上脚的 $2$ 可以走到的地方就是红色的,那么右上角数的父项就是左中的 $1$。
右上角数字的父项称作坏根。
hPrSS 的展开方式是,忽略上面一行坏根**及**以前的数字及其所连的边和下面一整行数字,然后将右上脚数字减 $1$,最后将还没有忽略的数字和边重复 $\omega$ 次,然后把忽略的边和数字填上,最后再根据规则在下面一行填上合理的数字。
例如,上面举的例子的展开就是:
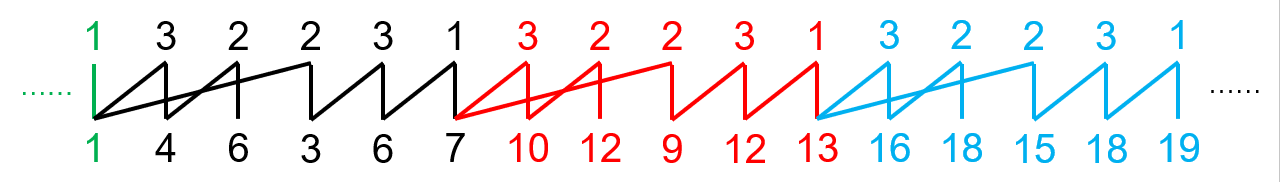
省略了前四项和后面若干项。
既然规则搞明白了就又可以开始扽西了。
以下表格将列出 OCF、hPrSS 表达式、Veblen、lPrSS 表达式。
| MOCF | hPrSS | Veblen | lPrSS |
| :--: | :--: | :--: | :--: |
| $<\psi(\psi(0))$ | Same as lPrSS |$<\varepsilon_{\varepsilon_0}$| $<(1,3,5)$ |
| $\psi(\psi(0))$ | $(1,3,4,6)$ | $\varepsilon_{\varepsilon_0}$ | $(1,3,5)$ |
| $\psi(\psi(\psi(0)))$ | $(1,3,4,6,7,9)$ | $\varepsilon_{\varepsilon_{\varepsilon_0}}$ | $(1,3,5,7)$ |
| $\psi(\Omega)$ | $(1,3,5)$ | $\zeta_0$ | $(1,4)$ |
| $\psi(\Omega2)$ | $(1,3,5,3,5)$ | $\zeta_1$ | $(1,4,4)$ |
| $\psi(\Omega\omega)$ | $(1,3,5,4)$ | $\zeta_\omega$ | $(1,4,5)$ |
| $\psi(\Omega^2)$ | $(1,3,5,5)$ | $\eta_0$ | $(1,5)$ |
| $\psi(\Omega^3)$ | $(1,3,5,5,5)$ | $\varphi(4,0)$ | $(1,6)$ |
| $\psi(\Omega^\omega)$ | $(1,3,5,6)$ | $\varphi(\omega,0)$ | $(1,(1,2))$ |
| $\psi(\Omega^\Omega)$ | $(1,3,5,7)$ | $\varphi(1,0,0)$ | $limit=(1,(1,(1,\dots)))$ |
| $\psi(\Omega^{\Omega\omega})$ | $(1,3,5,7,6)$ | $\varphi(\omega,0,0)$ |
| $\psi(\Omega^{\Omega^2})$ | $(1,3,5,7,7)$ | $\varphi(1@3)$ |
| $\psi(\Omega^{\Omega^\omega})$ | $(1,3,5,7,8)$ | $\varphi(1@\omega)$ |
| $\psi(\Omega^{\Omega^\Omega})$ | $(1,3,5,7,9)$ | $\varphi(1@(1,0))$ |
| $\psi(\Omega\uparrow\uparrow4)$ | $(1,3,5,7,9,11)$ | $\varphi(1@(1@(1,0)))$ |
| $\psi(\psi_1(0))$ | $(1,4)$ | $limit=\varphi(1@(1@(1@\dots)))$ |
| $\psi(\psi_1(1))$ | $(1,4,4)$ |
| $\psi(\psi_1(\omega))$ | $(1,4,5)$ |
| $\psi(\psi_1(\Omega))$ | $(1,4,6)$ |
| $\psi(\Omega_2)$ | $(1,4,7)$ |
| $\psi(\psi_2(0))$ | $(1,5)$ |
| $\psi(\psi_3(0))$ | $(1,6)$ |
| $\psi(\Omega_\omega)$ | $limits=(1,\omega)$ |
也就是说 hPrSS 的极限就是 $\psi(\Omega_\omega)$。
---
0-Y 对阶差序列的运用则更为充分,用到了多次求阶差的方式。
阶差序列意义同 hPrSS。
0-Y 山脉图的绘画方式如下:
不停的取阶差序列,直到父项等于末项减一。
展开方式如下:
将山脉图最上方按 hPrSS 最上方规则展开,然后和 hPrSS 一样复制、代回。
这里代回有一个特殊规则:如果坏部的某一项的父项位于坏根所在列之前,那么复制的时候只把靠右的边端点向右平移,靠左的边端点固定不变。
回忆一下 BMS 也有一个看上去莫名其妙的规则:如果一个元素的祖先项不包含坏根元素,那么复制的时候这个元素保持不变。
那么,这是否说明,BMS 和 0-Y 本质相同?
当然!不过这是后话。
和 BMS 一样,这条规则也是为了使 0-Y 停机,从而不会 ill-defined。
举个例子,$0-Y(1,5)$ 的展开。
先画出山脉图:
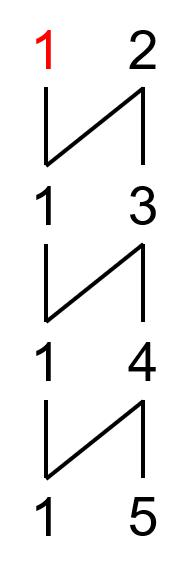
坏根已经标出。那么展开规则就是对右上元素的 $2$ 进行减一操作,然后无限重复,最后就是:
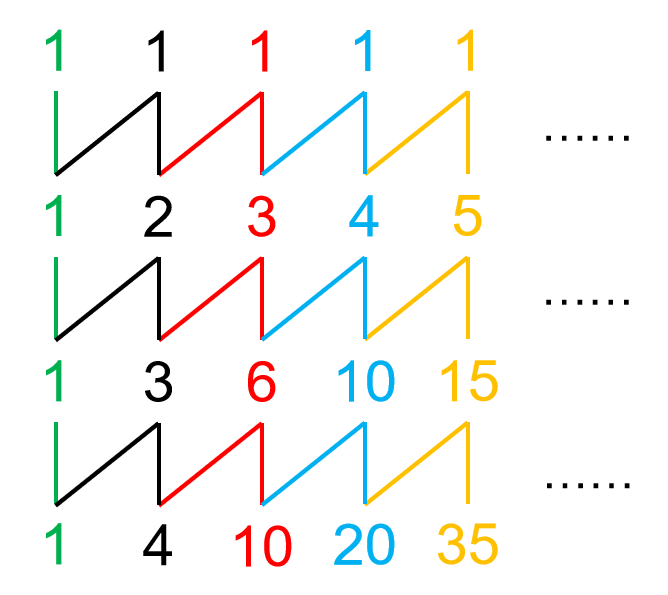
还有一个比较复杂的例子:$0-Y(1,4,6,4)$。
同样画出山脉图:
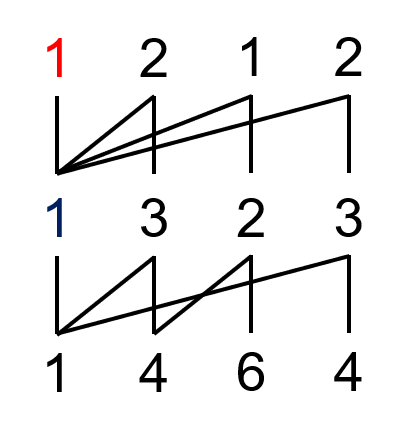
好部是 $1$,坏部是 $2,1,1$。无限重复代回,得到:
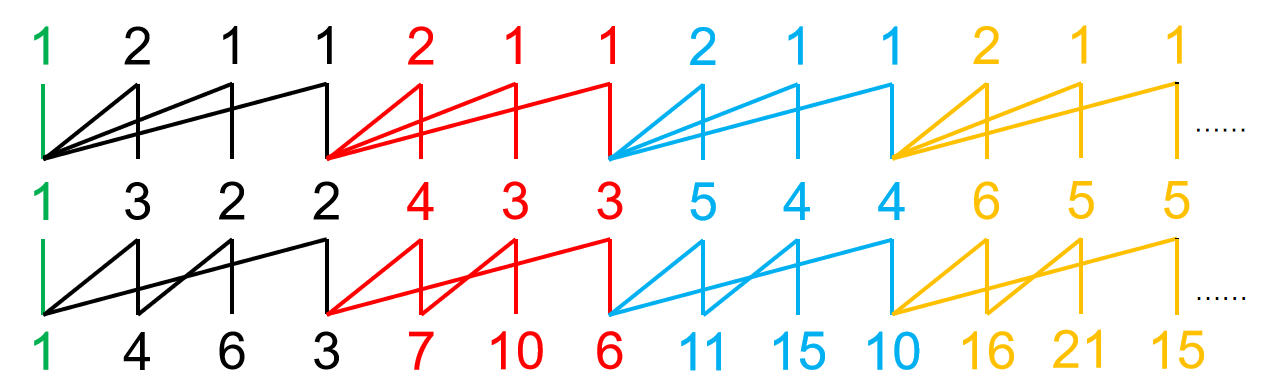
还有一个特殊规则的例子:$0-Y(1,4,6,3,7,9,7)$。
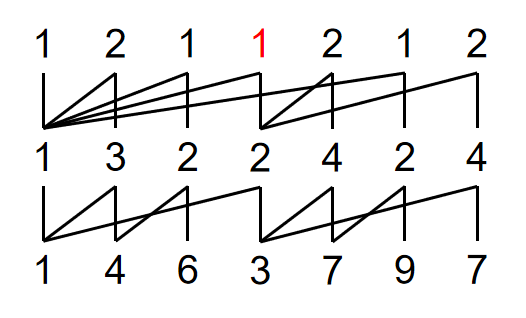
注意到中间一行第六项 $2$ 的坏根是中左 $1$,在第四列之前,所以对应的靠左边不变。那么,展开就是:
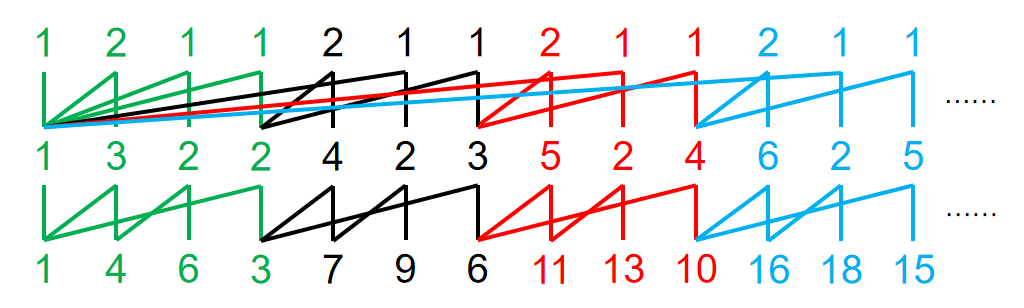
强度分析参考 BMS,接下来要讲的是 0-Y 和 BMS 的转换,然后就可以 BMS 方式扽了。
---
这一章山脉图的规则有点变化:再画一层,直到上层所有数全为 $1$。
举个例子,$0-Y(1,4,7,10,7,9,4,7,9,13,17,21,17,19,5)$。
我为什么举这个例子?当然是因为 Suzuka 梅天狸 举得这个。
多一层的山脉图:
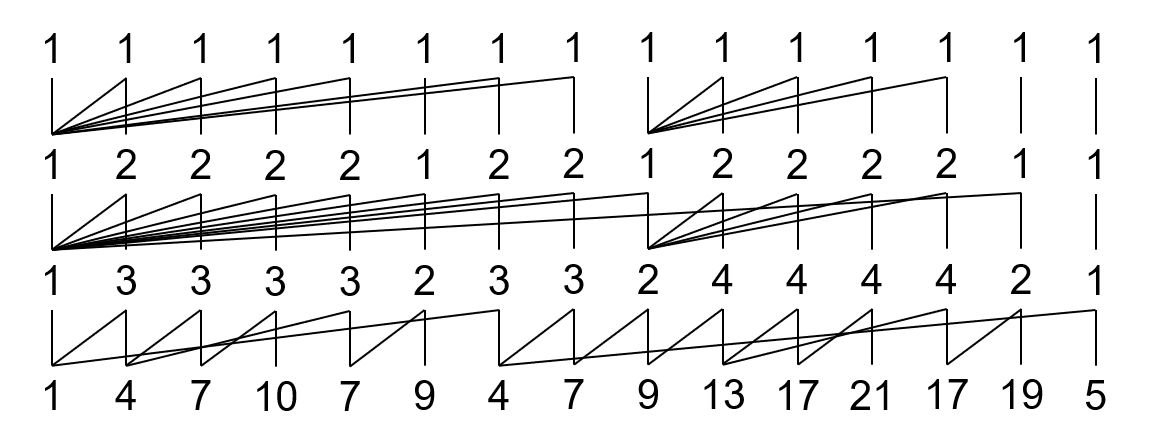
第一行的存在是帮助我们确定父项的,不用管他。
对于其他元素:
1. 所有 $1$ 的阶是 $0$;
2. 父项的阶为自己的阶减去 $1$。
比如说上面那个玩意就会转化为:
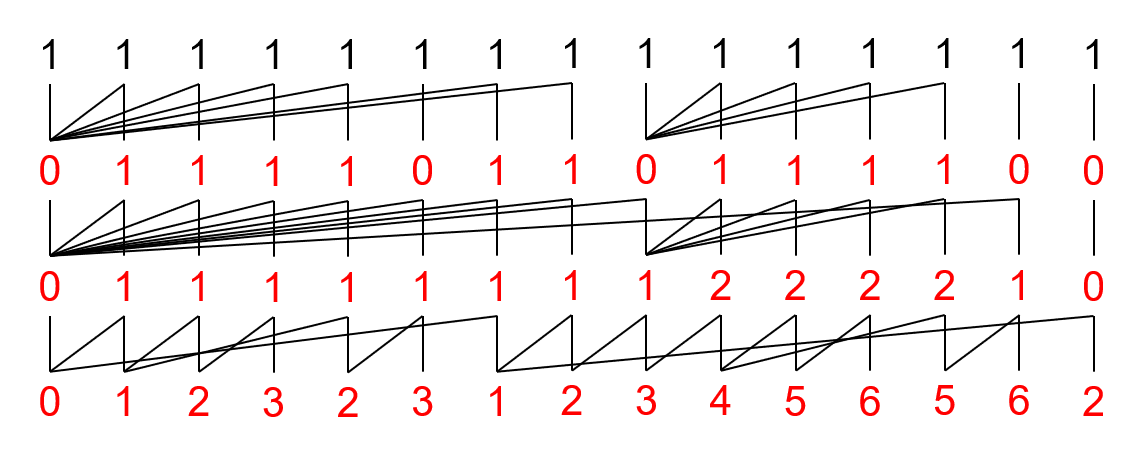
然后把每一行倒过来就是转化出来的 BMS:$(0)(1,1,1)(2,1,1)(3,1,1)(2,1,1)(3,1)(1,1,1)(2,1,1)(3,1)(4,2,1)(5,2,1)(6,2,1)(5,2,1)(6,1)(2)$。
于是,第九章结束了。