字符串匹配(KMP)
MarsTraveller
·
·
算法·理论
字符串匹配
字符串匹配算法有多种,目的是查找模式串在主串中第一次出现的位置。最常见的有 KMP 和 BM 算法。
规定待匹配串叫模式串,被匹配串叫主串。
为简化描述,我们规定主串长度为 n,用 \text{s[ ]} 表示。模式串长度为 m,用 \text{p[ ]} 表示。
一、KMP 算法:
1. 主要思想:
对比暴力算法,在匹配的时候能否优化呢?
假设从 c 点开始匹配,在 \text{p}[i] 匹配的时候失配了,思考模式串应向右移动到哪里呢?
由于是到 \text{p}[i] 时失配的,那么主串中的 \text{s}[c...c+i-1] = \text{p}[0...i-1]。
显然,盲目向右移动一位是无脑的。
既然我们已经知道了主串中 \text{s}[c...c+i-1] 段的字符,那么在这一段字符中,我们可以找一段字符串,使该字符串和模式串尽可能匹配,移动模式串和那个字串对齐,接着匹配。这样可以减少很多无用的比较。
如下图,是一个移动操作的示意:
显然,我们可以将该操作转换为一个问题:
找出一个字符串(长为 l)中的最长前缀,使其与后缀相等,该长度记为 h(h \ne l)。
比如串 ababa,他的 h 是 3。
为什么要求最长前缀?因为可能会漏情况(不解释了,太简单)。
2. 算法分析 ①(求 \text{pre}[\ ] 数组):
我们需要预处理出解决如上问题的数组 \text{pre[ ]}。
**根据定义:令 $k = \text{pre}[j]$ ,则 $\text{p}[0...k-1] = \text{p}[j-k...j-1]$。**
------------
若 $\text{p}[0...i-1]$ 没有相等的前缀和后缀,记 $\text{pre}[i] = 0$ 。
特别地,令 $\text{pre}[0] = -1$ (后面讲为什么)。
------------
**如何求 $\text{pre}[\ ]$ 数组呢?**
我们可以使用递推的思想。
考虑已经知道了 $\text{pre}[0...j]$,如何求出 $\text{pre}[j+1]$ 的值?
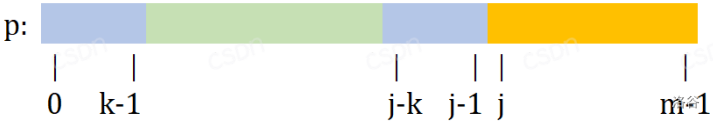

### (1)令 $k = \text{pre}[j]$。
根据定义,可知 $\text{pre}[0...k-1] = \text{pre}[j-k...j-1]$。
### (2)那么假如 $\text{pre}[k] = \text{pre}[j]$,显然可知 $\text{pre}[j+1] = \text{pre}[j]+1$。
------------
### (3)现在考虑 $\text{p}[k] \ne \text{p}[j]$ 的情况。
由于 $\text{pre}[0...k-1] = \text{pre}[j-k...j-1]$,我们可以直接舍去一段,转换成子问题求解。
对于串 $\text{p}[0....j-1]$,能否找到除 $\text{pre}[j]$ 外的,**第二小的满足前缀后缀相等的子串**,这样不会影响串 $\text{p}[0....j-1]$ 的性质。
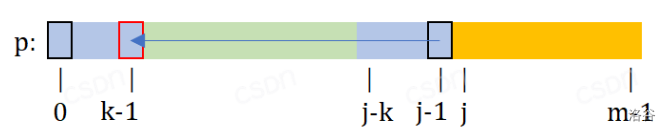
**由于我们寻找次小答案的时候,可以将次小后缀转移到最大前缀的后缀(如图中箭头)。**
**也就是在 $\text{p}[0....k-1]$ 中寻找最优前后缀相等子串,也就是 $\text{pre}[k]$。**
### (4)于是我们更新 $k = \text{pre}[k]$ ,再次判断 $\text{p}[k] = \text{p}[j]$,不成立则继续寻找次小答案。
当始终 $\text{p}[k] \ne \text{p}[j]$,最后一定 $k = 0$,此时一定有 $\text{p}[0] \ne \text{p}[j]$,倘若 $\text{pre}[0] = 0$ 则会一直陷入循环,所以我们可以将 $\text{pre}[0]$ 设为 $-1$,再加一个特判,防止这个问题。
同时,求 $\text{pre}[1]$ 时,由于 $k = \text{pre}[0] = -1$,跳出循环,直接赋值 $\text{pre}[1] = 0$。
```cpp
void init()
{
big j = 0;
big m = p.length(); // m是模式串p的长度
pre[0] = -1; // 初始条件
while(j < m-1) // 已知 pre[0...j],求 pre[j+1]。
{
big k = pre[j];
while(k != -1)
{
if(p[k] == p[j])
{
pre[++j] = k+1; // 匹配到了,更新数组
break;
}
else if(p[k] != p[j])
{
k = pre[k]; // 否则继续重复,寻找更次小前后缀
}
}
if(k == -1)
{
pre[++j] = 0; // 匹配不成功,pre[j+1] = 0
}
}
}
```
**我们对该代码进行优化,让其变得更加简洁:**
**合并 $k = -1$ 和 $\text{p}[k] = \text{p}[j]$ 两种情况。**
1. 当 $k = -1$ 时,应该让 `pre[++j] = 0`,这里 `k++` 刚好使得 $k = 0$ 。
2. 当 $\text{p}[k] = \text{p}[j]$ 时,需要 `pre[j++] = k+1` ,改成 `pre[j++] = k++`,直接更新 $k$,省去了 开始时 $k = \text{pre}[j]$ 的过程。
```cpp
void init()
{
big j = 0, k = -1, m = p.length();
pre[0] = -1;
while(j < m-1)
{
if(k == -1 || p[j] == p[k])
{
pre[++j] = ++k; // 更新了 k = pre[j]
}
else if(p[j] != p[k])
{
k = pre[k];
}
}
}
```
### 3. 算法分析②(KMP 主体):
如图,我们令一开始匹配的长度为 $j$ ,浅蓝色的部分长度为 $k = \text{pre}[j]$ ,$\text{p}[j]$ 与 $\text{s}[i]$ 失配。

此时我们需要移动模式串至 $j-k$ 的位置,也就是移动 $j-k$ 格。
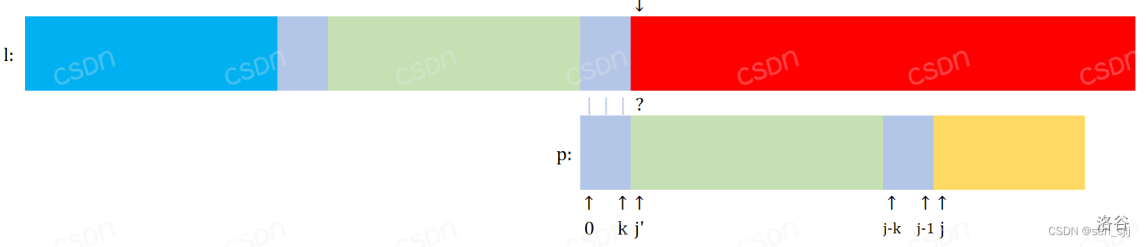
此时,$j' = k = \text{pre}[j]$。所以我们可以直接更新 $j = \text{pre}[j]$。
从 $\text{p}[j']$ 与 $\text{l}[i]$ 匹配开始,一直往下匹配,重复这个过程。
假如此时 $\text{pre}[j] = 0$,会判断 $\text{p}[0]$ 与 $\text{l}[i]$ 匹配,若仍不匹配,此时 $j = \text{pre}[0] = -1$,需要手动移动到下一位(也就是让 $\text{p}[0]$ 与 $\text{l}[i+1]$ 匹配,更新 $i = i+1$,$j=0$)。
```cpp
while(i < n && j < m)
{
if(j == -1) // 手动对齐
{
i++; j = 0;
}
if(s[i] == p[j]) // s[i]与 p[j] 匹配成功,继续往下
{
i++; j++;
}
else if(s[i] != p[j])
{
j = pre[j]; // 移动 p,继续递归。
}
}
if(j == m) // 匹配成功
{
return i-j;
}
```
**同样方法考虑优化:**
合并 $j = -1$ 和 $\text{s}[i] = \text{p}[j]$ 两种情况。其中 $j = -1$ 时 `++j`。
```cpp
big KMP()
{
big n = s.length(), m = p.length();
big i = 0,j = 0;
while(i < n && j < m)
{
if(j == -1 || s[i] == p[j])
{
i++, j++;
}
else if(s[i] != p[j])
{
j = pre[j];
}
}
if(j == m)
{
return i-j;
}
return -1;
}
```