支配树小记
xzf_200906
·
·
算法·理论
本文是不是应该放在算法·理论区?
upd on 2025.3.12:重新投稿至算法·理论区。
upd on 2025.3.23:修正了一个笔误并重新投稿,原来的文章已删除。
引入
给定一张 n 个点 m 条边的有向图 G 和一个点 s。定义点 u 支配节点 v 当且仅当所有从 s 到 v 的路径都经过节点 u。对于所有点求出有多少个点被它支配。
下文称 $u$ 支配 $v$ 为 $u\ dom\ v$,且默认 $s$ 能到达图上任何一个结点。
## 支配关系与支配树
此题的数据范围决定了我们不能暴力枚举每个点对并判断其中一个点是否支配另外一个点。这意味着我们必须分析支配关系的性质。不难发现这个关系显然满足传递性。因此考虑证明:
> #### Lemma 1
> 支配关系是偏序关系,即其满足传递性(若 $u\ dom\ v$,$v\ dom\ w$,则 $u\ dom\ w$),反对称性和自反性($u\ dom\ v$ 且 $v\ dom\ u$ 等价于 $u=v$),证明略。
上述性质说明支配关系除去自环外形成一张 DAG。但是 DAG 上可达点对计数的复杂度下界是 $\mathcal{O}(n^2)$ 的,不可做。考虑继续发掘性质:
> #### Lemma 2
> 若 $u\ dom\ w$ 且 $v\ dom\ w$,则 $u\ dom\ v$ 或 $v \ dom\ u$。
>
> 证明:假设命题不成立,则我们可以得出存在一条 $s\rightsquigarrow u$ 的不经过 $v$ 的路径。考虑将其与一条 $u\rightsquigarrow w$ 的简单路径拼在一起。则由于 $v\ dom\ w$,故其必定经过 $v$,即形如 $s\rightsquigarrow u \rightsquigarrow v \rightsquigarrow w$。同理我们可以得到一条 $s\rightsquigarrow v$ 的不经过 $u$ 的路径,把它和上面的 $v\rightsquigarrow w$ 拼接起来即可得到一条 $s\rightsquigarrow v \rightsquigarrow w$ 的不经过 $u$ 的路径,与 $u\ dom\ w$ 相矛盾,故假设不成立,原命题成立。
根据上述命题,对于每个点 $u\neq s$ 均存在恰好一个点 $idom(u)\neq u$ 满足其支配 $u$ 且不存在 $v$ 使得 $idom(u)\ dom\ v,v\ dom\ u$。如果对于每个 $u\neq s$ 将 $idom(u)$ 和 $u$ 连边,由于支配关系不会成环,我们会得到一棵以 $s$ 为根的外向树。则点 $u$ 支配点 $v$ 当且仅当在这棵树上 $u$ 是 $v$ 的祖先。如果我们将这棵树建出来,则 $u$ 的子树大小就是 $u$ 支配的点的数量。我们称这棵树为支配树。
## 构建支配树
考虑连通性相关问题中的经典工具——dfs 树。我们求出图中一棵以 $s$ 为根的 dfs 树并求出每个点的 dfs 序(下文称 $u<v$ 当且仅当 $u$ 的 dfs 序小于 $v$,其他同理)。则由于在这棵树上已经存在一条 $s\rightsquigarrow u$ 的路径,故 $idom(u)$ 必定是 $u$ 的祖先。并且对于 $u$ 的祖先 $v$,若其不支配 $u$,则必定存在一种从 $v$ 的某个祖先绕过 $v$ 到达 $u$ 的方式。由于我们不关心除 $u$ 的祖先以外的节点,所以我们考虑把 $u$ 的所有祖先全部拉出来组成一张新图 $G_u$。对于 $u$ 的两个祖先 $x,y$,若存在一条路径 $x=p_0\to p_1\to \cdots\to p_k=y$ 满足对于 $i\in [1,k-1]$ 有 $p_i$ 不是 $u$ 的祖先,则连一条边 $x\to y$。如下图:
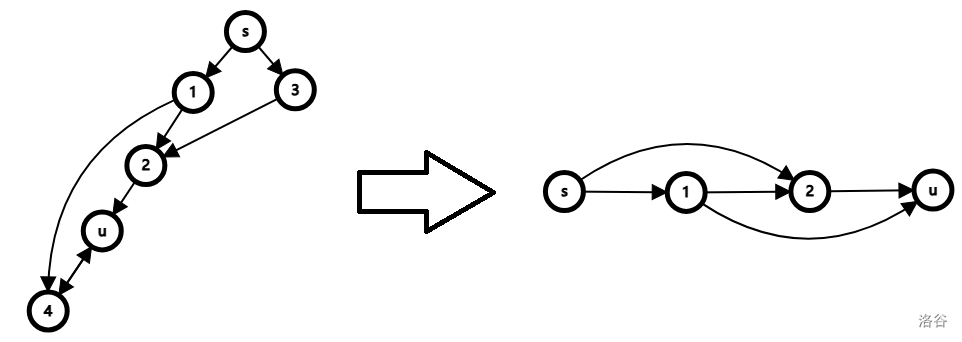
则有以下引理:
> #### Lemma 3
> $v$ 在 $G$ 中支配 $u$ 当且仅当 $v$ 在 $G_u$ 的点集中且 $v$ 在 $G_u$ 中支配 $u$。
>
> 证明:先证充分性,假设命题不成立,即在 $G$ 中 $v$ 不支配 $u$,则必定存在一条路径 $s=p_0\to p_1 \to \cdots \to p_k=u$ 不经过 $v$。则将其中不在 $G_u$ 中的点去掉即可得到一条在 $G_u$ 中且不经过 $v$ 的路径,则 $v$ 在 $G_u$ 中也不支配 $u$,与命题矛盾,故假设不成立,原命题成立。
>
> 再证必要性,根据前述讨论,$v$ 必须是 $u$ 的祖先。假设命题不成立,即在 $G_u$ 中存在一条不经过 $v$ 的 $s\rightsquigarrow u$ 的路径,则对于其中的每条边都替换成 $G$ 中对应的路径即可得出 $G$ 中的一条 $s\rightsquigarrow u$ 的路径。并且在此过程中不会加入 $u$ 的祖先,即该路径不包含 $v$,则 $v$ 在 $G$ 中也不支配 $u$,与命题矛盾,故假设不成立,原命题成立。
事实上,我们有更强的结论:
> #### Lemma 4
> $v$ 在 $G_u$ 中支配 $u$ 当且仅当 $G_u$ 中不存在边 $x\to y$ 使得 $x<v<y$。证明略。
这说明对于 $x\geq y$,$G_u$ 中 $x\to y$ 的边是没用的,下文将默认 $x<y$。同时也意味着 $idom(u)$ 就是在 $G_u$ 中不被任意一条边覆盖的点中最大的那个。但是这样的边还是太多了,不方便分析。考虑若 $G_u$ 中某个点有多个入度,则只有最小的那一个有用。不过 $u$ 在所有 $G_i$ 中不一定有相同的入度。但是不难发现若 $G_u$ 包含边 $v\to u$,则在其转移到 $u$ 在 dfs 树上的儿子 $son$ 时,这条边可能变为 $v\to son$,但是起点必定不变且终点必定不会回退(证明见下文 Lemma 5)。则记 $G_u$ 中最小的入度为 $u$ 的半支配点或 $sdom(u)$。形式化地说,对于任意 $u\neq s$,$sdom(u)=\min\{v|\exists v\to u\in G_u\}$。
> 注意,此处对 $sdom$ 的定义与其它题解中的定义有出入,但可以证明它们是等价的。
既然边 $sdom(u)\to u$ 不会回退,则 $(sdom(u),u)$ 内的所有点在任意 $u$ 的后代 $v$ 的 $G_v$ 中均被覆盖。那么我们猜想是不是对于所有的点 $p$,$G_p$ 中只有 $sdom(u)\to u$ 有用呢?先引出两个引理。
> #### Lemma 5
> 对于所有的 $v$ 满足 $u$ 是 $v$ 的祖先,$G_v$ 中必定包含一条 $sdom(u)\to w$ 的边满足 $w\geq u$。
>
> 证明:考虑 $G_u$ 中的边 $sdom(u)\to u$,若 $G$ 中该边对应的路径不经过 $w\in (u,v]$,则 $G_v$ 中也存在边 $sdom(u)\to u$。否则取路径上最前面的点 $w$,则 $w>u$ 且 $G_v$ 上必定存在一条边 $sdom(u)\to w$。
> #### Lemma 6
> 若 $u$ 是 $v$ 的祖先且 $G_v$ 中存在 $x\to y$ 满足 $y\leq u$,则 $G_u$ 包含 $x\to y$。证明略。
有证明:
> #### Lemma 7
> 定义 $G'_u$ ,其点集为 $u$ 的所有祖先,边集为 $\{sdom(u)\to u\}$,则 $G_u$ 中不存在边 $x\to y$ 使得 $x<v<y$ 当且仅当 $G'_u$ 中不存在边 $x\to y$ 使得 $x<v<y$。**注意,这不代表 $G'_u$ 和 $G_u$ 的支配关系等价!**
>
> 证明:若 $G'_u$ 中 $v$ 被覆盖,则存在一个点 $w$ 满足 $sdom(w)<v<w$。则根据 Lemma 5,$G_u$ 中必定存在一条边 $sdom(w)\to p$ 满足 $p>v$。反之,若 $G_u$ 中 $v$ 被覆盖,则存在一条边 $x\to y$ 满足 $x<v<y$。则根据 Lemma 6,$G_y$ 中必定存在一条边 $x\to y$,故 $sdom(y)\leq x<v<y$。则命题得证。
现在这张图的性质已经非常好了,因为每个点只有一条入边,且这条入边在所有的 $G'_i$ 中都是相同的。考虑直接用这张图求解答案。假设我们求出了所有的 $sdom$,如何利用它求出 $idom(u)$?由于 $G'_u$ 中存在边 $sdom(u)\to u$,则区间 $(sdom(u),u]$ 中的节点均不满足条件。若这个区间中不存在一个 $v$ 满足 $sdom(v)<sdom(u)$,则说明 $sdom(u)$ 没有被任意一条边覆盖,故 $idom(u)=sdom(u)$。否则,贪心地找到使得 $sdom(v)$ 最小的点 $v$,再对 $(sdom(v),u]$ 做一遍类似的操作,直到找到这样一个区间为止,如下图,其中 $idom(v)=sdom(v)$。
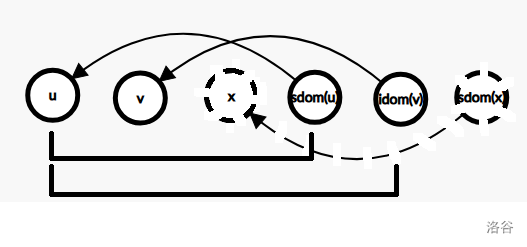
但是暴力做上面的操作是不优的。由于 $G'_v$ 中的边必定在 $G'_u$ 中,我们是否可以已经计算出的 $idom(v)$ 来优化 $idom(u)$ 的计算呢?事实上有结论:
> #### Lemma 8
> 若 $G'_u$ 中存在 $v\in (sdom(u),u]$ 满足 $sdom(v)<sdom(u)$,设 $v$ 是其中使 $sdom(v)$ 最小的一个,则 $idom(u)=idom(v)$。
>
> 证明:先证明 $idom(v)\ dom\ u$,即 $G'_u$ 上不存在一条边 $sdom(x)\to x$ 满足 $sdom(x)<idom(v)<x$。假设存在这样的边,则由于 $G'_v$ 中不存在这样一条边,故 $u\geq x>v>sdom(u)$。又因为 $G'_v$ 中存在边 $sdom(v)\to v$,故 $sdom(v)\geq idom(v) > sdom(x)$,则 $sdom(x)<sdom(v)$,且 $x\in (sdom(u),u]$。与 $sdom(v)$ 最小矛盾,故假设不成立,原命题成立。详见上图。
>
> 再证明不存在 $w$ 满足 $idom(v)\ dom\ w,w\ dom\ u$,即不存在一个点 $w>idom(v)$ 满足 $w$ 在 $G'_u$ 中未被覆盖。
> + 若 $w\leq v$,由于 $idom(v)\neq w$,则 $G'_v$ 中必定存在一条边 $sdom(x)\to x$ 满足 $sdom(x)<w<x$,且其显然在 $G'_u$,则 $w$ 被这条边覆盖。
> + 若 $w>v>sdom(u)$,则由于 $G'_u$ 中存在边 $sdom(u)\to u$,故 $w$ 被这条边覆盖。
>
> 综上所述,$idom(u)=idom(v)$。
根据上述讨论,只需要求出 $sdom(u)$ 并计算出对于每个 $u$ 在 dfs 树上的链 $sdom(u)\rightsquigarrow u$(不包括 $sdom(u)$)中的点的 $sdom$ 的最小值及使其取到最小值的位置即可从上到下计算 $idom(u)$。由于链上最值是简单的,故下文将讨论 $sdom$ 的求法。
## 求解半支配点
> 注意,本文对 $sdom$ 的定义与其它题解中的定义有出入,详见上文,但可以证明它们是等价的。
考虑如何求出点 $u$ 的半支配点 $sdom(u)$,其必定有一条不经过 dfs 树上链 $sdom(u)\rightsquigarrow u$ 的路径。枚举其除 $u$ 外的最后一个端点 $v$,分以下两种情况:
#### Case 1:$v$ 是 $u$ 的祖先
此时这条路径必定不经过其它点。故令 $sdom(u)\gets \min(sdom(u),v)$。
#### Case 2:$v$ 不是 $u$ 的祖先
设 $l$ 为 dfs 树上 $u$ 和 $v$ 的 lca,则这条路径必定是从 $u$ 的某个祖先 $p$ 开始,除此之外不经过 $u$ 的祖先,到达链 $l\rightsquigarrow v$(不包括 $l$)中的某个节点 $w$,再从这个节点到达 $v$,最后到达 $u$,如下图。
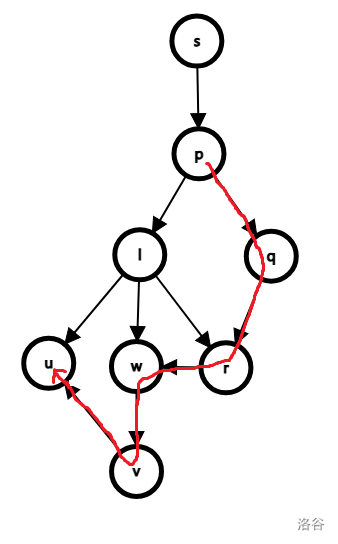
如果 $p$ 是 $l$ 的祖先,则 $G_w$ 上必定有边 $p\to w$。考虑证明这一点。有一个众所周知的引理:
> #### Lemma 9
> 对于图上的一条横叉边 $u\to v$,有 $u>v$。
>
> 证明:假设 $u<v$,则在 dfs 遍历 $u$ 时必定尚未遍历 $v$。由横叉边的定义,$u,v$ 间不存在子孙后代关系,故在遍历完毕 $u$ 的子树后 $v$ 也尚未遍历,此时 $u\to v$ 会成为一条树边,与条件矛盾。故假设不成立,原命题成立。
> #### Lemma 10
> 满足上述条件的 $p$ 必定为 $l$ 的祖先。
>
> 证明:假设条件不成立,则 $l$ 是 $p$ 的祖先且 $l\neq p$。设其最小的大于 $l$ 的祖先为 $x$,$w$ 满足该条件的祖先为 $y$,则由于 $u<v$,故 $x<y$。考虑路径上第一个不小于 $y$ 的点 $b$,它的上一个点为 $a$,则有 $a<b$。根据 Lemma 8,$a\to b$ 是一条前向边或树边,故 $a$ 是 $b$ 的祖先。又因为 $a<y\leq b$,则 $a$ 是 $y$ 的祖先且 $a\neq y$。故 $a$ 是 $l$ 的祖先,也是 $u$ 的祖先。与条件矛盾。故假设不成立,原命题成立。
根据上述引理,$G_w$ 上必定有边 $p\to w$,且仿照上述证明可得任意边 $p\to w$ 在 $G$ 上对应的路径不经过 $u$ 的祖先。故若 $G_w$ 上有边 $p\to w$ 则 $p$ 满足条件。其中最小的一者显然为 $sdom(w)$。则只需要令 $sdom(u)\gets \min(sdom(u),sdom(w))$ 即可。根据 Lemma 9 不难得出 $v$ 不是 $u$ 的祖先当且仅当 $v>u$。故有以下公式:
$$\small sdom(u)=\min(\{v|\exists v\to u,v<u\}\cap\{sdom(w)|\exists v\to u,v>u , w 是 v 的祖先且 w\in(l,v]\})$$
但是这就说明求解 $sdom(u)$ 需要先求解 $sdom(w)$,需要确定一个转移顺序。幸运的是,由于 $v>u$,故 $w>u$,所以只需按 dfs 序从大到小求解 $sdom$ 即可。
## 算法设计
然而用树剖求链上最值并不优美,我们希望有一个更好的算法。先考虑求解 $sdom$ 时用到的树上最值。暴力算法的过程肯定是从枚举到的点开始,暴力向上跳到第一个不大于 $u$ 的节点,并计算经过的节点(不包含最终跳到的那个)的最小值。我们发现,随着算法的进行,可以跳到的位置肯定是越来越多,即若一个时刻可以从 $v$ 跳到点 $p$,那么以后都可以到达这里。于是我们考虑用一种数据结构存储信息以免重复计算。联想到边带权并查集,我们可以设计以下步骤:
1. 当遍历到一个点 $u$ 时,枚举其入度 $v$,若 $v<u$ 则可以简单维护,否则令 $sdom(u)$ 在其本身和 $v$ 到其所在并查集的根的链上最小值之间取较小值。
2. 在并查集中从点 $p$ 向其在 dfs 树上的父亲之间连一条边权为 $sdom(p)$ 的边。
使用路径压缩即可方便地优化该算法。
再考虑求 $idom$ 的部分,由于其需要求出 dfs 树上 $sdom(u)$ 和 $u$ 之间的链上最小值(及其位置),于是我们可以将点 $u$ 挂在 $sdom(u)$ 上,每次在处理点 $u$ **之前**枚举 $sdom(v)=u$ 的点 $v$,由于 $u$ 是 $v$ 的祖先,故此时 $v$ 在并查集中的根就是 $u$。则可以方便地求出链上最小值所在的位置 $w$。若 $sdom(w)<u$,那么计算 $idom(v)$ 就要用到 $idom(w)$,但是此时 $idom(w)$ 尚未计算。为了解决这个问题,可以新开一个并查集,在其中加入边 $v\to w$,表示 $idom(v)=idom(w)$。最后找到每个点在该并查集中的根即可完成计算。
具体实现可以参考代码,由于并查集仅使用路径压缩的单次访问时间复杂度为 $\mathcal{O}(\log n)$(存疑),故整体时间复杂度为 $\mathcal{O}(m\log n)$。
## Code
```cpp
#include <bits/stdc++.h>
#define LL long long
using namespace std;
vector<int> e[1000000],er[1000000],poi[1000000];
int fa[1000000],minn[1000000],minp[1000000];
struct Info{
int p,val,pos;
};
Info find(int p){
if(fa[p]){
Info ret=find(fa[p]);
fa[p]=ret.p;
if(minn[p]>ret.val){
minn[p]=ret.val;
minp[p]=ret.pos;
}
return {fa[p],minn[p],minp[p]};
}
return {p,(int)1e9,0};
}
int faT[1000000],dfn[1000000],pos[1000000],tot=0;
bool vis[1000000];
void dfs(int p){
dfn[p]=++tot;
pos[tot]=p;
vis[p]=1;
for(auto it:e[p]){
if(!vis[it]){
faT[it]=p;
dfs(it);
}
}
}
int sdom[1000000],idom[1000000];
int findIdom(int p){
if(idom[p]!=p) return idom[p]=findIdom(idom[p]);
return p;
}
int siz[1000000];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
er[v].push_back(u);
}
memset(minn,0x3f,sizeof(minn));
dfs(1);
for(int i=tot;i>=1;i--){
int p=pos[i];
for(auto it:poi[p]){
if(find(it).val<dfn[p]) idom[it]=find(it).pos;
else idom[it]=it;
}
if(i==1) break;
sdom[p]=1e9;
for(auto it:er[p]){
if(dfn[it]<=dfn[p]) sdom[p]=min(sdom[p],dfn[it]);
else sdom[p]=min(sdom[p],find(it).val);
}
poi[pos[sdom[p]]].push_back(p);
fa[p]=faT[p];
minn[p]=sdom[p];
minp[p]=p;
}
for(int i=2;i<=tot;i++) findIdom(pos[i]);
for(int i=2;i<=tot;i++) idom[pos[i]]=pos[sdom[idom[pos[i]]]];
for(int i=tot;i>=1;i--){
siz[pos[i]]++;
if(i!=1) siz[idom[pos[i]]]+=siz[pos[i]];
}
for(int i=1;i<=n;i++) cout<<siz[i]<<' ';
cout<<'\n';
return 0;
}
```