【硬核】集合论 - 序数 - 第十二章 - ω-Y
Butterfly_qwq
·
·
算法·理论
这是这一系列的第十二章,第十一章在这。
接下来,是 ω-Y 的主场!
我们考虑把提取规则去掉,来获取更为厉害的表现。
和 1-Y 一样,先来说几个 ω-Y 的式子来表示它的强大:
\omega-Y(1,3,10)=Y(1,4)
\omega-Y(1,4)=Y(1,\omega)
这还仅仅是体现 \omega-Y 强大的一小部分规则,一般的我们有 \omega-Y(1,n+3)=C\ n-Y(1,\omega)。
至于 C\ Y 和 D\ Y 的区别,暂且不表。只需要知道,我们上一篇讲的 Y 既是 C\ 1-Y 也是 D\ 1-Y(然而从结构上来看是 C\ 1-Y),D 比 C 发明要晚,结构几乎一致,并且强度还要弱。
那要它有什么用?
当然有用。适当的弱化是为了向无限推广,C 模式是不能走向无限的,也就是说,\omega-Y 只有 D\ \omega-Y 一种。
actual magma 是 $\omega-Y$ 刚被发明出来的时候的规则,难于理解。
事实上这些的区别在于 magma 边。定义 magma 边的时候有 weak magma 和 strong magma。展开 magma 边的时候有 weak recursion 和 strong recursion。
weak magma 是 weak magma+weak recursion。
actual magma 是 weak magma+(有时候 weak recursion 有时候 strong recursion),这也是 actual 最难于理解的原因。
medium magma 是 weak magma+strong recursion。
strong magma 是 stong magma+strong recursion。
靠后的比靠前的强大,但是极限都是一样的,清一色 MHO。所以基本上大家所说的 $\omega-Y$ 都是理解最容易的 weak magma,本文接下来所讲的就是这些。
说了这么多……
你 TM 赶紧说 ω-Y 序列是啥啊!
---
先来说一下 ω-Y 山脉图画法吧。
大部分定义与 1-Y 相同。
在 ω-Y 中,有一个叫做行标的东西。
其实 1-Y 也有这个东西,不过不很重要。
简单来说,行标 $\alpha$ 和 $\alpha+\omega^k$ 用 $k$ 条横线隔开。
也就是说,一条横线分割 $\omega$ 系数不同的区域,两条横线分割 $\omega^2$ 系数不同的区域……
省流:$\sum\limits_{i=0}^{+\infty}\alpha_i\omega^i$ 的行标下边有 $\alpha_i$ 条 $i$ 重线(你猜为什么是 $+\infty$ 不是 $\omega$)。
如果一个元素的行标是 $\alpha$,父项行标是 $\beta$,且 $\beta+\omega^k\le\alpha<\alpha+\omega^{k+1}$,那么阶差的行标就是 $\beta+\omega^{k+1}$。
然后开始画就行了。
举个例子:$\omega-Y(1,5,26,134,115,284)$。
在看下面之前,大家可以先自己画一画。
完整山脉图是这样的。
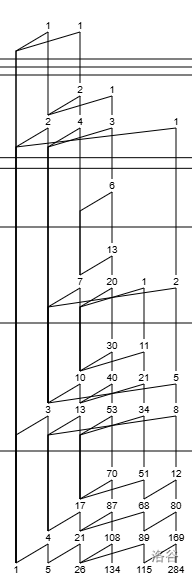
Suzuka梅天狸说一列一列的画比一行一行的画更方便,我试了,深以为不然,因为经常会把本应在线下面的元素画到线的上面。
---
接下来该讲展开了。
我们定义:
1. 根元素、根列同 1-Y;
2. 根列元素:位于根列且行标小于等于根元素的元素;
3. 作用区域:一个根列元素的作用区域为行标范围为它自己(含)到下一个根列元素(不含)的所有元素;
4. eruption 边(轮廓边):从一个根列元素开始,不超过作用范围的向右上走一步,不超过作用范围的向左下走若干步,可能经过的所有边就是 eruption 边;
5. wildfire 边(非轮廓边):作用区域内不是 eruption 边就是 wildfire 边;
6. magma 边(填充边):从一个根列元素开始,不超过作用范围的向右上走一步,不超过作用范围的向左下走一步,可能经过的所有边就是 magma 边。
注意这里的非轮廓边和 1-Y 中的平移边并不一致。
规则:
1. 从上到下以作用区域为单位执行以下操作。
2. 把末列减一。
3. 提升 eruption 边:把 eruption 边向右平移的同时向上提升,提升的高度是根元素与末列最上方元素的行标之差。即:设 $\alpha$ 为根元素行标,$\beta$ 为末列上方元素行标,$\gamma$ 为满足 $\alpha+\gamma=\beta$ 的序数,那么原先行标为 $\delta$ 的将会平移到 $\gamma+\delta$。注意不是 $\delta+\gamma$。
4. 填充 magma 边:将上一步产生的空隙用 magma 边填补。当然如果没有空隙就不填补。
5. 平移 wildfire 边:左边的边不动,右边的边向右上平移。如果右边的边正下元素没有被 eruption 边指到,那么只向右平移,否则行为和 eruption 边一致。
比如说 $\omega-Y(1,4,8,18,48,32)$。
第一步,标出根元素和作用区域:
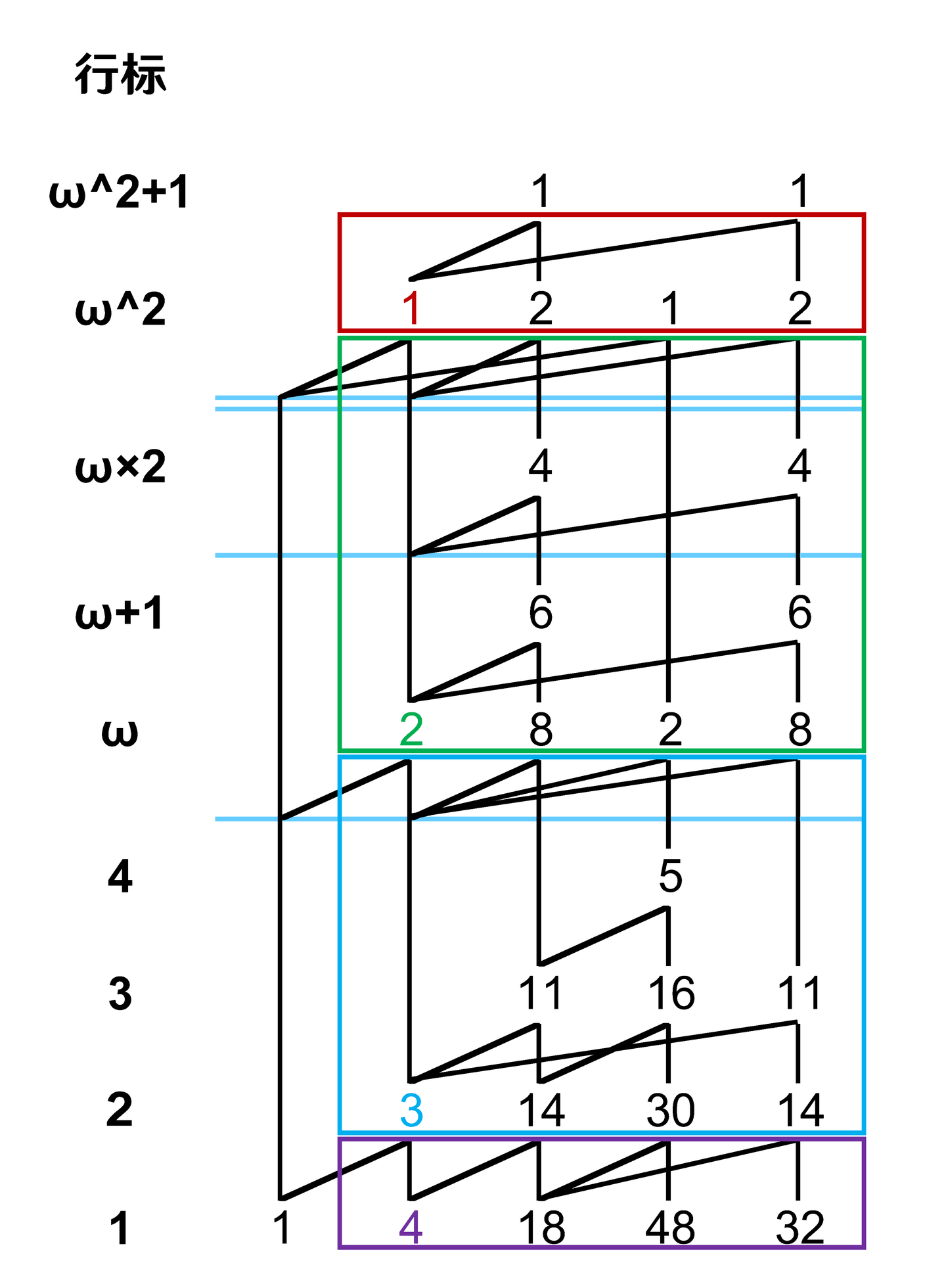
第二步,展开上层,因为只有一行,所以只用向右平移:
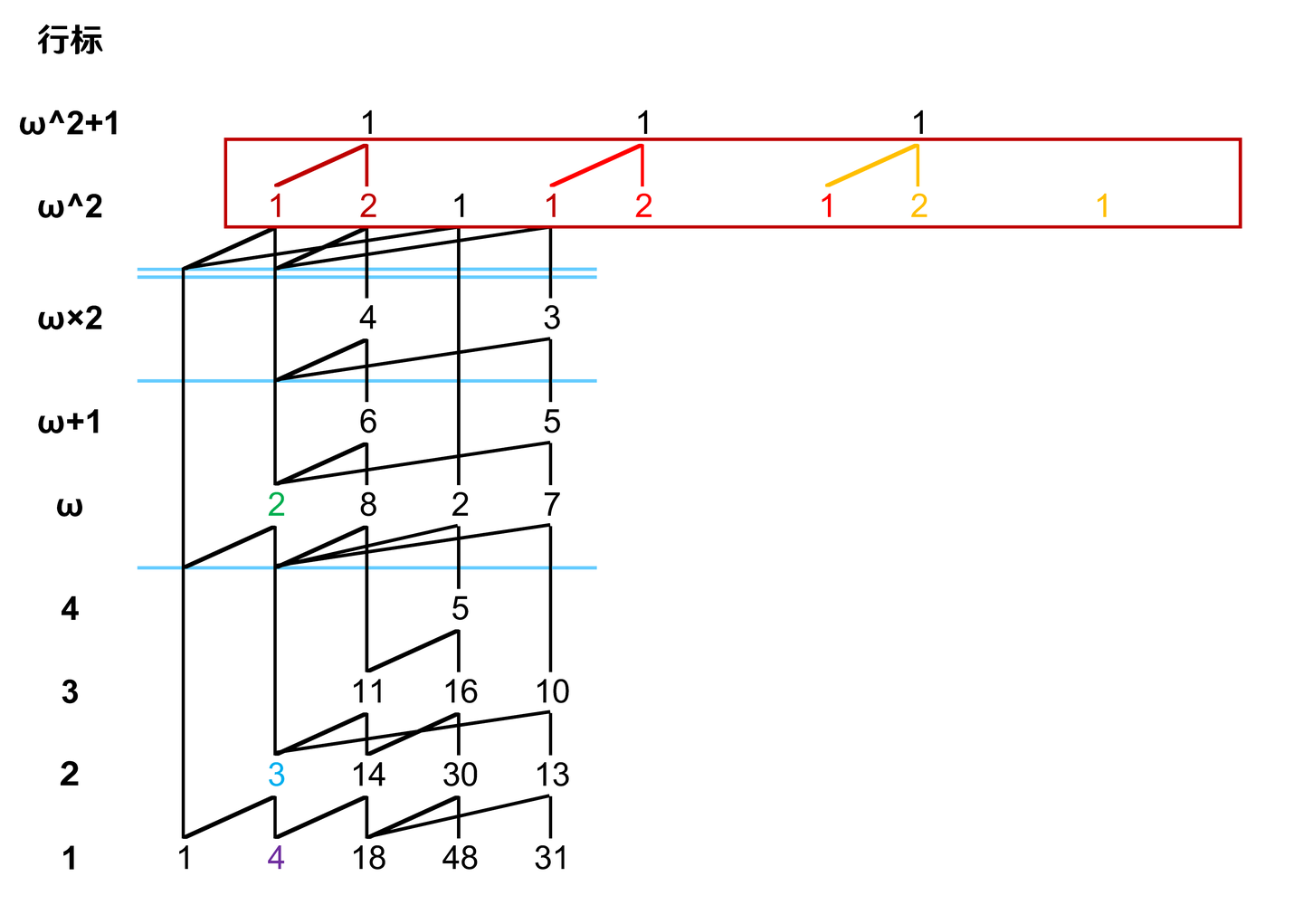
第三步,标记第二层 eruption 边并复制:
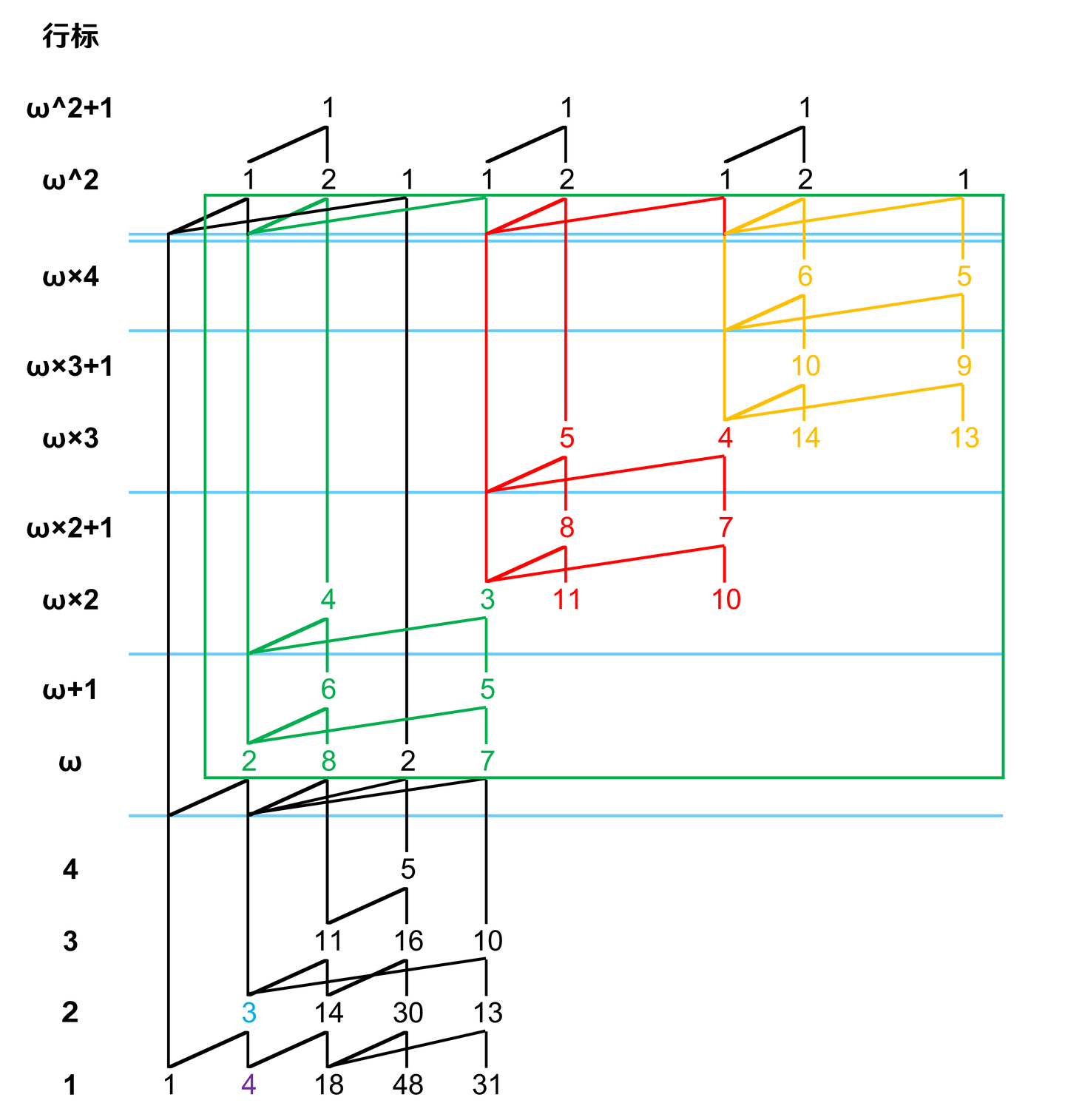
第四步,标记第二层 magma 边并填充:
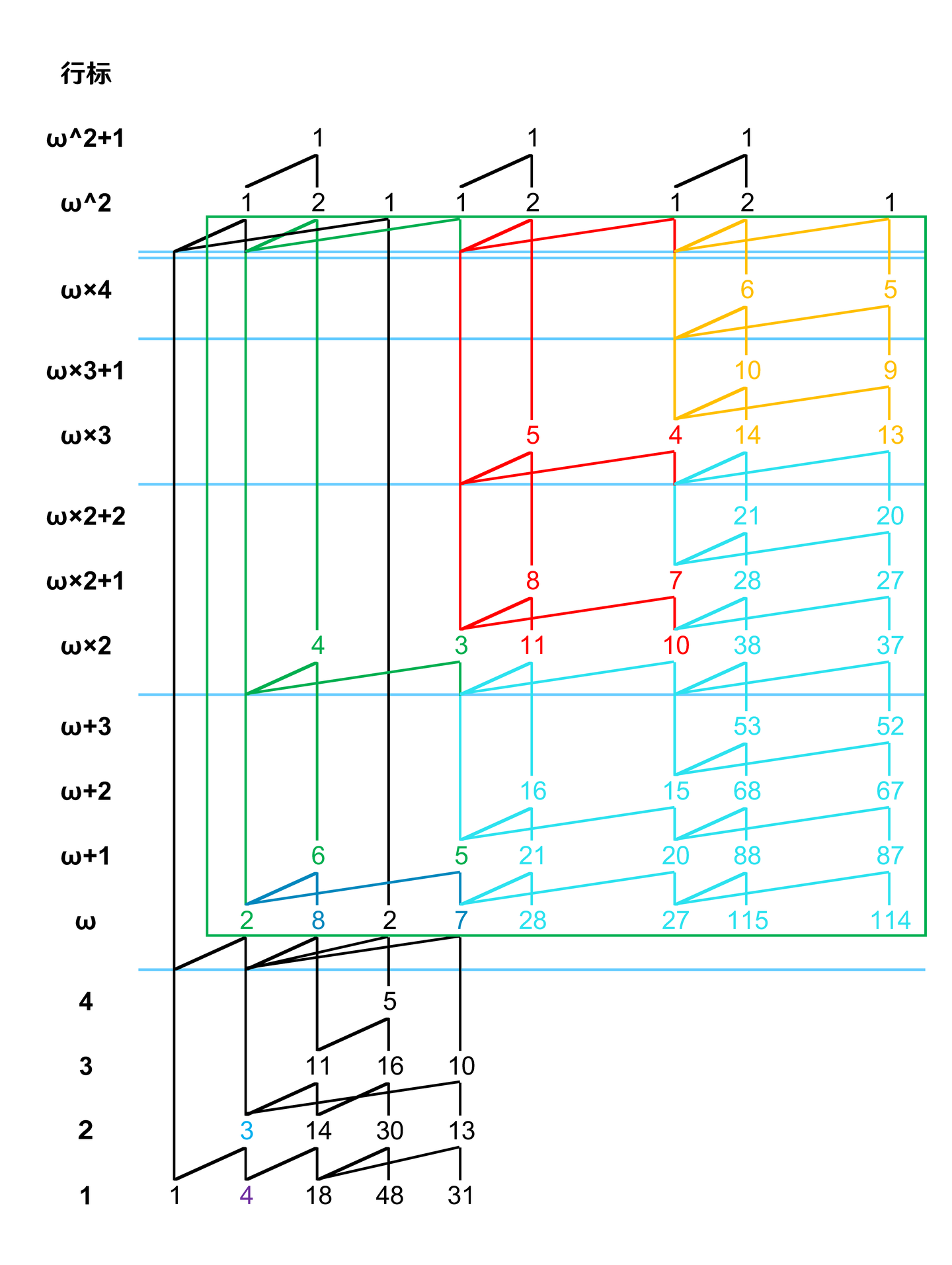
第五步,平移 wildfire 边:
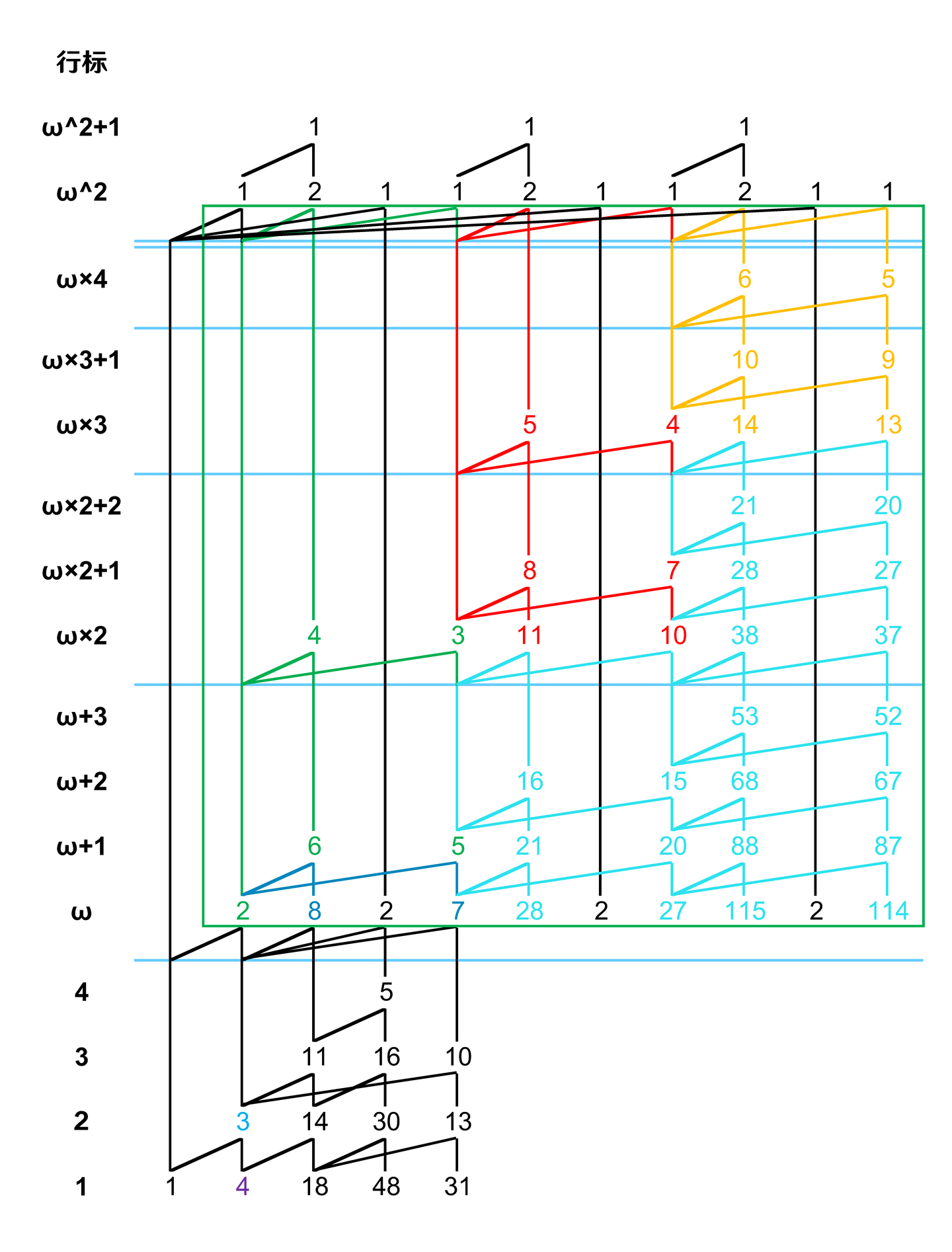
第六步,按着同样的操作复制最后两层:
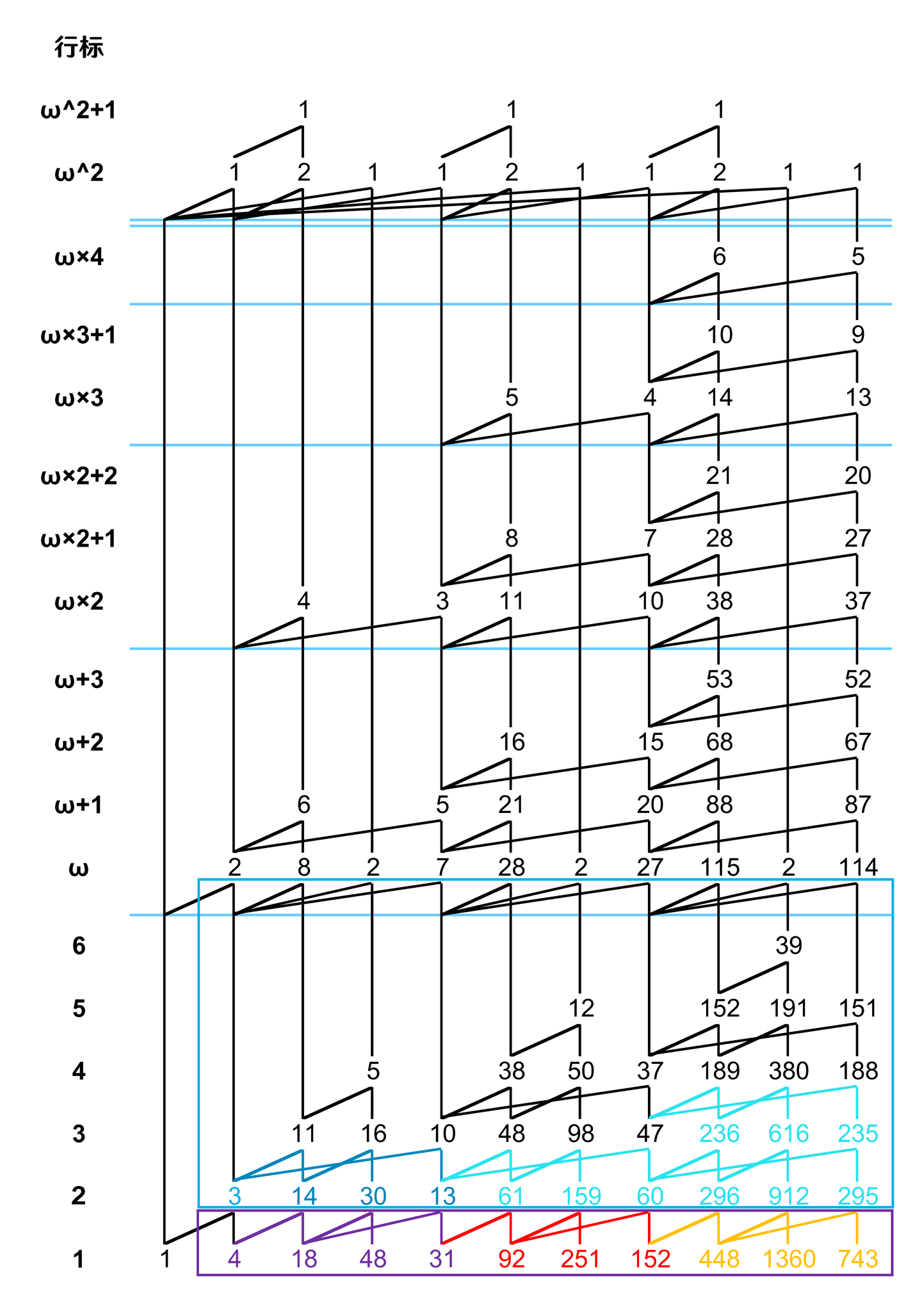
大功告成
---
作业:展开 $\omega-Y(1,5,26,134,115,284)$。
答案山脉图:

答案:$\omega-Y(1,5,26,134,115,283,572,1163,2974,10830,49037,233124,1085084,4874560,\dots)$。
---
对于 ω-Y,我们仍然没有很多的手段进行分析,作为对比,_没有什么可以对比的了_。
以后要讲的记号大多都是和 ω-Y 进行对比分析,比如 MMS、ωMN、fffz、X-Y。也就是说,ω-Y 是过不去的一关。但是由于上述记号和 ω-Y 均有错层效应导致分析
但是之前讲的记号远远不够描述 ω-Y 有多强,也许有一天会有一个强度在 1-Y 和 ω-Y 之间的简单记号来辅助了解。目前我找到的符合这样一个条件的记号是 DBMS,但是由于资源限制,我找不到其规则。
还是写几条吧?
$$\omega-Y(1,3,10)=Y(1,4)$$
$$\omega-Y(1,3,10,37)=Y(1,5)$$
$$\omega-Y(1,3,10,37,151)=Y(1,6)$$
$$\omega-Y(1,4)=Y(1,\omega)=C\ 2-Y(1,3)$$
$$\omega-Y(1,4,20)=C\ 2-Y(1,4)$$
$\omega-Y(1,n+3)$ 的展开式前 $k$ 位是 $C\ n-Y(1,k+1)$。
然后放几个我个人的想法。
注意到所有 worm 型记号大小都是字典序,只不过有一些不合法而已,也就是说,如果所有都合法呢?
很神奇的现象出现了!这样能表示的序数数量最多 $\omega^\omega$!
究其根本,还是因为本质上 $\omega$ 和任何可数序数都是可以一一对应的,包括 $\varepsilon_0,\Gamma_0,\varphi(1@(1,0)),\psi(\Omega_\omega),TSSO,QSSO,SHO,\Omega SSO,SYO,MHO$,甚至 $\Omega,\omega_1^{CK}$ 等等,第一个无法和 $\omega$ 一一对应的序数是 $\omega_1$,这也是第一个不可数序数。
所以,事实上上面说的是,worm 极限(也许是 LHO)和 $\omega^\omega$ 一一对应,明显说了等于没说。并且,这个记号是明显不良记号,也就是说如果有一天真的存在了这样的记号,必须要良序。由良序定理这可以一试,但是我怀疑如果真的存在这样的记号,极限也不过是 $\omega^\omega$。
但是为什么即使是最基本的 worm 型序列——PrSS(其实最基本的是 -4-Y,不过没意义),也超过了 $\omega^\omega$ 呢?
好问题,我不知道。
你问我为什么说这么多,当然是不想把 5w 字重任给我还没有完全搞懂的 ωMN。所以现在就堂堂 5w 字了。