Trie 从入门到入土
lkjzyd20
·
·
算法·理论
Tags: 字典树,Trie 字符串
字典树
前言
字典树,形如其名,像字典的树。
核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它支持快速存储字符集合,快速查询字符集合,快速修改字符集合是否存在。
如何构建
先放一张图
我们可以发现字典树的性质
那么,请你画出下面字符串的字典树
-
\tt ba
-
\tt bag
-
\tt ban
-
\tt bat
-
\tt bi
-
\tt big
-
\tt bil
-
\tt bit
应该就是这个样子:
我们使用 C++ 代码来构建它:
//son[][]存储子节点的位置,分支最多26条;
//cnt[]存储以某节点结尾的字符串个数(同时也起标记作用)
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26],cnt[N],idx;
char str[N];
int change(char s){return s-'a';}
void insert(char *str){
int p=0; //指向当前节点
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]); //将字母转化为数字
if(!son[p][u])son[p][u]=++idx; //该节点不存在,创建节点
p=son[p][u]; //使 p 指向下一个节点
}
++cnt[p]; //结束时的标记,也是记录以此节点结束的字符串个数
}
查询其实也差不多:
int query(char *str){
int p=0; //指向当前节点
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]); //将字母转化为数字
if(!son[p][u])return 0; //该节点不存在,即该字符串不存在
p=son[p][u]; //使 p 指向下一个节点
}
return cnt[p]; //返回字符串出现的次数
}
如何删掉呢?
void del(char *str){
int p=0; //指向当前节点
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]); //将字母转化为数字
if(!son[p][u])return 0; //该节点不存在,即该字符串不存在
p=son[p][u]; //使 p 指向下一个节点
}
--cnt[p]; //减少这个字符串出现的次数
}
然后做
- P10470 前缀统计
- PKU2503 Babelfish
- Poj3630 Phone List
- HDU1251 统计前缀
- Shortest Prefixes
35 分钟吧,不会做的可以问我。
Trie 的批量删除(度熊查单词)
百度的题目,挺新奇的,需要另一种思路维护删除操作(当然还有其他思路)。
void del(char *str){
int p=0;
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]);
if(!son[p][u])return;
p=son[p][u];
}// 查询是否有该前缀
p=0;
int t;
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]);
t=p;
p=son[p][u];
--cnt[p];//前缀减去
}
son[t][change(str[(int)strlen(str)-1])]=0;//该点清零
}
另外,我发现网上的题解大多是错的(迷惑行为)???
原因在于大多数题解是直接删掉了所有节点,代码是这样的:
void del(char *str){
int p=0;
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]);
if(!son[p][u])return;
p=son[p][u];
}
int ans=cnt[p];p=0;
rep(i,0,(int)strlen(str)-1){
int u=change(str[i]);
cnt[p]-=ans;
p=son[p][u];
}
rep(u,0,25)son[p][u]=0;
}
这会导致下一次无法继续扫到该节点,所以会出错。
[USACO08DEC] Secret Message G
给出 N 个 \tt01 串和 M 个 \tt 01串,问这 M 个串的每一个串中满足和这 N 个串其中的一个串有着相同的前缀(前者是后者的前缀或后者是前者的前缀)的数量。
思路:稍微的变形,我们记录一个 end_p 表示有多少个以当前节点为结尾的字符串,再记录一个 cnt_p 表示路过这个节点的字符串有多少个,注意,结尾和路过不要同时记录,然后查询时直接统计 end_p 和 cnt_p 即可。
#include <bits/stdc++.h>
// #define int long long
#define rep(i, l, r) for(int i = l; i <= r; ++ i)
#define per(i, r, l) for(int i = r; i >= l; -- i)
using namespace std;
const int N=1000010;
int son[N][2],cnt[N],ed[N],idx;
int s[N];
void insert(int *s){
int p=0;
rep(i,1,s[0]){
int u=s[i];
if(!son[p][u])son[p][u]=++idx;
if(p)++cnt[p];
p=son[p][u];
}
++ed[p];
}
int query(int *s){
int p=0,sum=0;
rep(i,1,s[0]){
int u=s[i];
if(!son[p][u])return sum;
p=son[p][u];
sum+=ed[p];
}
return sum+cnt[p];
}
main(){
int n,m;cin>>n>>m;
rep(i,1,n){
cin>>s[0];
rep(j,1,s[0])cin>>s[j];
insert(s);
}
rep(i,1,m){
cin>>s[0];
rep(j,1,s[0])cin>>s[j];
cout<<query(s)<<'\n';
}
}
为什么记录这题呢,因为这个题它同时考察了两种最常用的标记方法,挺典型的。
然后思维题:SP694,思考一下 trie 的本质。
模拟题:子串统计
给你一个长度为 N 的 01 字符串,然后问你在它的所有子串中,那些出现次数大于 1 次的子串的出现次数。
输出的顺序按子串本身的字典序,例如假设 01 这个子串出现 3 次,011 这个子串出现 2 次,则先输出 3 再输出 2
思路:暴力统计,dfs 输出即可
时限为 20 分钟。
开始进阶
01-trie 树可以用来维护一堆数字的异或和,支持修改(删除+重新插入),和全部维护值加一。
友情提示:下面题目难度为 ????
The XOR Largest Pair
这题好像是蓝书的例题,嗯,确实挺典型的。
在给定的 N 个整数 A_1,A_2,…,A_N 中选出两个进行异或运算,得到的结果最大是多少?
我们先把每个数给转化为 32 位二进制数,接着思考如何选。我们可以发现,只有二进制数位数越多才能选,然后前面异或时尽量都为 \tt1。则使 A_i 与其异或值最大的整数一定是高位至低位与 A_i 有尽可能多的不同位(使异或结果可以尽可能多地获得 \tt1)。
字典树开数组注意计算(纯靠运气)!!!
#include <bits/stdc++.h>
//#define int long long
#define rep(i, l, r) for(int i = l; i <= r; ++ i)
#define per(i, r, l) for(int i = r; i >= l; -- i)
using namespace std;
const int N=10000010;
int n,A[N];
int son[N][2],idx,ans;
void insert(int x){
int p=0;
per(i,31,0){
int k=(x>>i)&1;
if(!son[p][k])son[p][k]=++idx;
p=son[p][k];
}
}
int query(int x){
int p=0,ans=0;
per(i,31,0){
int k=(x>>i)&1;
if(!son[p][k^1])p=son[p][k];
else p=son[p][k^1],ans^=(1<<i);
}
return ans;
}
main()
{
cin>>n;
rep(i,1,n){
cin>>A[i];
insert(A[i]);
}
rep(i,1,n){
ans=max(ans,query(A[i]));
}
cout<<ans;
return 0;
}
Pku3764 The xor-longest Path
给定一棵 n 个点的带权树,求树上最长的异或和路径。
思路:其实跟上一题差不多,预处理出每一个节点到根的异或和就可以了。
「一本通 2.3 例 3」Nikitosh 和异或
求出两个不同区间 A,B,使得 A 的异或和加上 B 的异或和最大。
首先,我们知道区间 [l,r] 的异或和可以表示为 [1,l] \oplus [1,r],那么我们可以设 S1_i 表示区间 [1,i] 的最大异或和,S2_i 表示区间 [i,n] 的最大异或和,用 Trie 维护一下即可。
main(){
cin>>n;
rep(i,1,n){
cin>>A[i];
insert(A[i]);
s1[i]=max(s1[i-1],query(A[i]));
}
memset(son,0,sizeof 0);
idx=0;
per(i,n,1){
insert(A[i]);
s2[i]=max(s2[i+1],query(A[i]));
}
rep(i,1,n-1){
ans=max(ans,s1[i]+s2[i+1]);
}
cout<<ans;
return 0;
}
[JOI Open 2016] 销售基因链 / Selling RNA Strands
建议去 luogu 交,有全部数据。
题意:给定 n 个文本串 S_i,有 m 次询问,每次给定两个字符串 P,Q,求有多少个文本串同时包含前缀 P 和后缀 Q。
题解区的做法都看不懂,除了这篇抽象的启发式题解,以下是原题解。
首先,对前缀和后缀分开考虑。要求的值即为 Trie 树上指定的前缀对应的点的子树内有多少串的后缀等于指定的后缀。
于是我们建一个 Trie,插入每个串 $S_i$ 并在其对应位置上开一个哈希表,当作桶存储 $S_i$ 的每个后缀的哈希值。之后,我们离线操作,把每个操作挂在这个操作的前缀在 Trie 上对应的点上(如果没有这样的点答案就是 $0$,直接忽略)。
接着,我们对 Trie 进行 DFS。对于每个点,先遍历其儿子,并在过程中维护当前点及其已经遍历的子孙的后缀组成的桶。对于每个新遍历的儿子,将当前的桶与该儿子的桶进行启发式合并,即遍历其中较小的桶,并将其中的元素加入另一个桶。遍历完所有儿子后,我们就可以处理当前点上的询问,每个询问的答案即为询问的后缀在桶中的出现次数。
容易证明,时间复杂度为 $O((\sum|S_i|)\log(\sum|S_i|))$,略微精细处理即可轻松通过本题,跑得飞快(没在最优解最后一页)。
我感觉看完就能懂,以下是我的补充:
+ 虽然时间复杂度是对的,但是具有较大的常数,所以需要使用一些手段卡常。
+ 注意哈希处理的时候以及它所加入的节点。
还有一道强制在线的题:bzoj 4212: 神牛的养成计划,本人能力有限,不予讲解。
```cpp
#include <bits/stdc++.h>
#include <bits/extc++.h>
//#define int long long
#define rep(i, l, r) for(int i = l; i <= r; ++ i)
#define per(i, r, l) for(int i = r; i >= l; -- i)
using namespace std;
using namespace __gnu_pbds;
const int N=2e6+10,M=1e5+10,base=233331;
int n,m;
char s[N];
int son[N][4],idx,ff[N],tot,ans[N];
unsigned int q[N];
cc_hash_table<unsigned int,int>mp[M];
std::vector<int> V[N];
int change(char ss){
if(ss=='A')return 0;
if(ss=='G')return 1;
if(ss=='U')return 2;
if(ss=='C')return 3;
}
void insert(){
int p=0,n=strlen(s)-1;
rep(i,0,n){
int u=change(s[i]);
if(!son[p][u])son[p][u]=++idx;
p=son[p][u];
}
if(!ff[p])ff[p]=++tot;
unsigned int v=0;
per(i,n,0)v=v*base+s[i],mp[ff[p]][v]++;
}
void query(int id){
int p=0,n=strlen(s)-1;
rep(i,0,n){
int u=change(s[i]);
if(!son[p][u])return;
p=son[p][u];
}
V[p].push_back(id);
}
int dfs(int u){
rep(i,0,3){
if(son[u][i]){
int v=dfs(son[u][i]);
if(!ff[u]){
ff[u]=v;
continue;
}
if((int)mp[ff[u]].size()<(int)mp[v].size())swap(ff[u],v);
for(auto &i:mp[v])mp[ff[u]][i.first]+=i.second;
mp[v].clear();
}
}
for(auto i:V[u])if(mp[ff[u]].find(q[i])!=mp[ff[u]].end())ans[i]+=mp[ff[u]][q[i]];
return ff[u];
}
main()
{
cin>>n>>m;
rep(i,1,n){
cin>>s;
insert();
}
rep(i,1,m){
cin>>s;
query(i);
cin>>s;
int len=strlen(s)-1;
per(j,len,0)q[i]=q[i]*base+s[j];
}
dfs(0);
rep(i,1,m)cout<<ans[i]<<'\n';
return 0;
}
```
## 可持久化 Trie
这些图都来自于 $AcWing$。
现在我们对于 $\tt cat,rat,cab,fry$ 进行可持久化 Trie。
这是普通的 Trie:
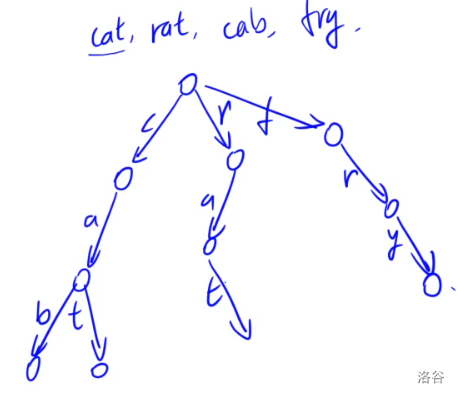
对于 $\tt cat$ 的所建第一棵 Trie:

对于 $\tt rat$ 的所建第二棵 Trie:
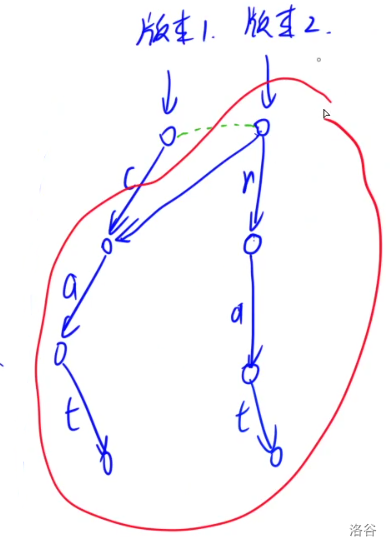
对于 $\tt cab$ 的所建第三棵 Trie:
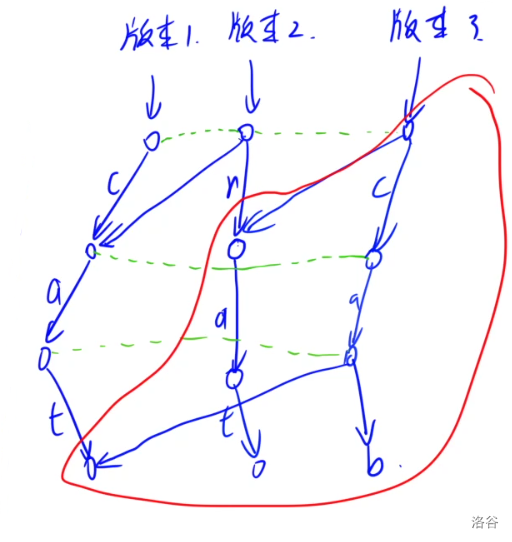
对于 $\tt fry$ 的所建第四棵 Trie:
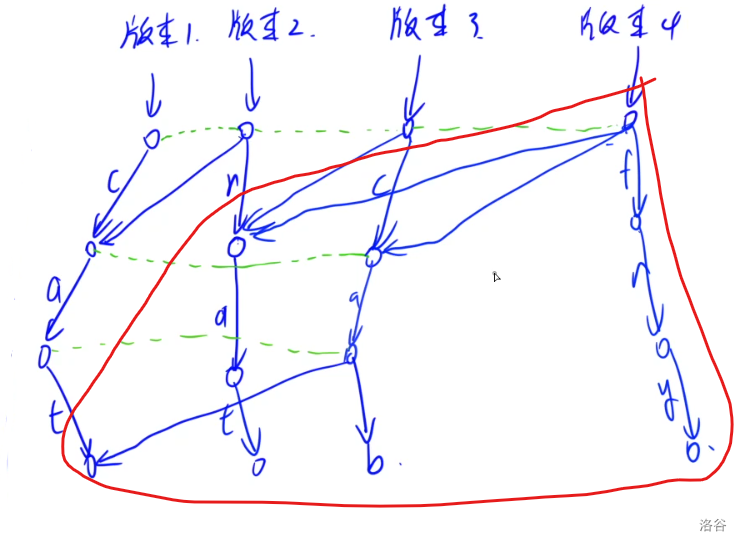
我们发现,这样建立 Trie,每一次只会新增插入字符串 $|S|$ 个节点,而其他的节点则没有修改。对于每个版本的 Trie,从该版本的根节点出发所能访问到的所有节点构成的一棵 Trie 树,就是 $a_i\sim a_i$ 全部插入之后形成的一棵 Trie 树,但大大节省了空间和时间。
### 最大异或和
给定一个非负整数序列 $\{a\}$,初始长度为 $N$,有 $M$ 个操作,有以下两种操作类型:
+ `A x`:添加操作,表示在序列末尾添加一个数 $x$,序列的长度 $N$ 加 $1$。
+ `Q l r x`:询问操作,你需要找到一个位置 $p$,满足 $l \le p \le r$,使得:$a[p] \oplus a[p+1] \oplus ... \oplus a[N] \oplus x$ 最大,输出最大值。
思路:令 $s_i=a_1\oplus a_2 ...\oplus a_i$,对于题中所给的对一段区间的询问,我们就可以转化为前缀异或,即$a_p\oplus a_{p+1} ...\oplus a_n\oplus x=s_{p-1}\oplus s_n\oplus x$。这样,问题就转化为了在给定的区间 $[L,R]$ 中,求出与 $s_n\oplus x$ 异或的答案最大的数。
如何查询区间 $[L,R]$ 内和 $s_n\oplus x$ 异或起来最大的数?
首先根据可持久化 Trie 的性质,从第 $i$ 个版本的根节点出发能访问到的节点构成了第 $i$ 个版本的 Trie。所以可以先从第 $i$ 个版本的根节点出发,这样就满足了 $R$ 的上界限制。我们再记录一个 $maxid$ 表示这颗子树最后被哪一个版本所更新过。
对于这道题,我们像建可持久化线段树一样建可持久化 Trie。
这个讲了递归版本和插入:https://www.acwing.com/solution/content/51419/
```cpp
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
// 30w初始数据和30w新增, 而10的7次方小于2的24次方, 再加上根节点, 就是说每个数最多需要25位;
const int N = 600010, M = N * 25;
int n, m;
int s[N]; // 前缀和序列
int tr[M][2];
int max_id[M]; // 用于记录当前根节点版本的最大id范围, 更直白的说就是当前点对应要存的数的在前缀和数组s的位置
int root[N], idx;
// i是第i个插入的数的i, p是上一个插入的数的节点号, q是当前节点号, k是现在取到第k位
void insert(int i, int k, int p, int q)
{
// 如果记录结束了
if (k < 0)
{
max_id[q] = i; // 记录当前节点(可能会被后面公用)所能到达的最大范围i
return;
}
// 取出前缀和的二进制表示从右往左数第k位v
// 需要注意的是, 这个s[i]就是我们要存的东西!!!!!
int v = s[i] >> k & 1;
// 如果前一个节点存在当前节点没有的分支, 那就把当前节点的这个空的路径指过去, 这就相当于复制!
if (p) tr[q][v ^ 1] = tr[p][v ^ 1];
tr[q][v] = ++idx; // 现在才是正常trie树插入
// 递归插入下一位二进制, tr[q][v]就是我们本轮插入的新节点
// 而前面我们只复制了前一轮的不同v方向的路径, v方向的还没动过, 于是放到p里面等下一轮
// 至于为什么可以放到下一轮, 因为当前q新插入的数字(二进制当前位)是v, 而p的这条路径也是v
// 所以暂时不需要复制
insert(i, k - 1, tr[p][v], tr[q][v]);
// 下面是递归到所有点都插入完成才开始进行的, 所以能把最大max_id递归传递回去
// 每个点的最大范围用子节点最大的值, 然后还能递归传递回去, 因为当前递归层
// 的q, 就是上一层的tr[q][v], 观察易知每个节点都会有对应max_id
max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]);
}
int query(int l, int r, int C)
{
// 选用合适的root, 就是第r-1个节点作为root(-1已在传参前完成)
// 然后根据异或的前缀和性质才能保证在r左边
int p = root[r];
for (int i = 23; i >= 0; i--)
{
// C是s[n] ^ x, 从高位到低位逐位检索二进制每一位上能跟C异或结果最大的数
int v = C >> i & 1;
// 自带判空功能如果没有点, max_id会为-1, 那就肯定不能满足>=l (根据初始化max_id[0] = -1)
// 如果没有这个初始化, max_id[0] 默认为0, 而当l=0 的时候就会令到p误跳到空节点
// 而max_id又同时可以限制当前的点是在l r区间内
// 另外, 如果tr[p][v^1]为空, 那么tr[p][v]就肯定不为空,并在l r区间, 因为根据
// 插入的代码, 每个节点至少有一条当前s[i]的完整路径
// 而如果tr[p][v^1]不为空但maxid小于l, 同理也能选取到tr[p][v]
// printf("max_id[%d]: %d, p: %d, l: %d\n", tr[p][v ^ 1], max_id[tr[p][v ^ 1]], p, l);
if (max_id[tr[p][v ^ 1]] >= l) p = tr[p][v ^ 1];
else p = tr[p][v];
}
return C ^ s[max_id[p]];
}
int main()
{
scanf("%d%d", &n, &m);
// 前缀和, 初始化root[0]
max_id[0] = -1;
root[0] = ++idx;
insert(0, 23, 0, root[0]);
for (int i = 1; i <= n; i++)
{
int x;
scanf("%d", &x);
s[i] = s[i - 1] ^ x; // 前缀和序列
root[i] = ++idx;
insert(i, 23, root[i - 1], root[i]);
}
char op[2];
int l, r, x;
while (m--)
{
scanf("%s", op);
if (op[0] == 'A')
{
scanf("%d", &x);
n++;
s[n] = s[n - 1] ^ x;
root[n] = ++idx;
insert(n, 23, root[n - 1], root[n]);
}
else
{
scanf("%d%d%d", &l, &r, &x);
printf("%d\n", query(l - 1, r - 1, s[n] ^ x));
}
}
return 0;
}
作者:abc喵
链接:https://www.acwing.com/solution/content/51419/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
```
这个是循环版本:
```
++n;
rt[n]=++idx;//新建一个版本节点
insert(k,rt[n-1],rt[n]);//插入
void insert(int k,int last_p,int p){//k 代表是当前版本编号,last_p 代表是上一个版本的根节点,p 代表是这个版本根节点。
per(i,23,0){
max_id[p]=k;
int v=(s[k]>>i)&1;
if(last_p)tr[p][v^1]=tr[last_p][v^1];//如果上一个版本的节点还有东西,其他的就继承。
tr[p][v]=++idx;//自己插入的新建。
p=tr[p][v];last_p=tr[last_p][v];//下一个节点。
}
max_id[p]=k;
}
```
### [省选联考 2020 A 卷] 树
题意:给定一棵树上每个结点的权值 $v_i$,定义 $val_u$ 为 $u$ 的子树(含 $u$)内的结点 $c_i$ 的 $v_{c_i}+d(c_i,u)$ 的异或和。求 $\sum\limits_{i=1}^nval(i)$ 。
要求维护一个集合,支持全局加一,查询全局异或和,合并。
要全局加一,考虑从低位往高位插入。这样加一的时候,对于遍历到的节点执行以下两个操作即可:
+ 交换左右子树
+ 往左子树递归
```cpp
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for(int i = l; i <= r; ++ i)
#define per(i, r, l) for(int i = r; i >= l; -- i)
using namespace std;
const int N=525020;
int n,v[N];
vector<int> V[N];
struct E{
int dep,ch[2],sum,val;
}t[N*100];
int rt[N],tot,res;
void push_up(int p){
t[p].sum=t[t[p].ch[0]].sum+t[t[p].ch[1]].sum;
t[p].val=t[t[p].ch[0]].val^t[t[p].ch[1]].val;
if(t[t[p].ch[1]].sum&1) t[p].val^=(1<<t[p].dep);
}
void insert(int &p,int v,int d){
if(!p){
p=++tot;
t[p].dep=d;
}
if(d>=26){
t[p].sum++;
return;
}
insert(t[p].ch[(v&(1<<d))>0],v,d+1);
push_up(p);
}
void change(int p){
if(!p) return;
swap(t[p].ch[0],t[p].ch[1]);
change(t[p].ch[0]);
push_up(p);
}
void merge(int &a,int &b){
if(!a){
swap(a,b);
return;
}
if(!b) return;
t[a].sum+=t[b].sum;
t[a].val^=t[b].val;
merge(t[a].ch[0],t[b].ch[0]);
merge(t[a].ch[1],t[b].ch[1]);
}
void dfs(int u){
rt[u]=++tot;
for(auto v:V[u]){
dfs(v);
merge(rt[u],rt[v]);
}
change(rt[u]);
insert(rt[u],v[u],0);
res+=t[rt[u]].val;
}
main(){
cin>>n;
rep(i,1,n)cin>>v[i];
rep(i,2,n){
int x;
cin>>x;
V[x].push_back(i);
}
dfs(1);
cout<<res;
return 0;
}
```
## [十二省联考 2019] 异或粽子
这是一类套路题,在这里给出一种简单的做法。
题意:求前 $k$ 大区间异或和。
https://www.luogu.com.cn/article/6tblywn6
我们很容易求出前缀异或和,则求一个区间的异或和变成两个前缀异或和的异或和,因为 $a_i \oplus a_j=a_j\oplus a_i$,且 $a_i \oplus a_i =0$,所以题目被转化为求第 $2k$ 大的异或有序对,我们把结果扔到堆里,每次取堆顶即可。
```cpp
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for(int i = l; i <= r; ++ i)
#define per(i, r, l) for(int i = r; i >= l; -- i)
using namespace std;
struct E{
int id,rk,val;
};
bool operator<(const E& a,const E& b){
return a.val<b.val;
}
priority_queue<E>q;
const int N=20000010;
int tr[N][2],sz[N],idx,n,m,s[N];
void insert(int x){
int p=0;
per(i,31,0){
++sz[p];
int v=(x>>i)&1;
if(!tr[p][v]) tr[p][v]=++idx;
p=tr[p][v];
}
++sz[p];
}
int query(int x,int rk){
int p=0,ans=0;
per(i,31,0){
int v=(x>>i)&1;
if(!tr[p][v^1])p=tr[p][v];
else{
if(rk<=sz[tr[p][v^1]])ans|=(1ll<<i),p=tr[p][v^1];
else rk-=sz[tr[p][v^1]],p=tr[p][v];
}
}
return ans;
}
main(){
cin>>n>>m; m*=2;
rep(i,1,n){
cin>>s[i]; s[i]^=s[i-1];
}
rep(i,0,n){
insert(s[i]);
}
rep(i,0,n){
q.push({i,1,query(s[i],1)});
}
int ans=1;
rep(i,1,m){
E t=q.top();ans+=t.val;q.pop();
if(t.rk<n)q.push({t.id,t.rk+1,query(s[t.id],t.rk+1)});
}
cout<<ans/2<<endl;
return 0;
}
```