凸性优化
AC_Lover
·
·
算法·理论
Slope Trick
理论
**重要性质:** 两个凸函数的和也是凸函数
**常用技巧:**
- 维护转折点,通常用堆,一个转折点$x$出现$k$次表示转折时斜率变化值为$k
例题
例一:P4597 序列 sequence - 洛谷
简要题意: 给定长度为 n 的数列 a,一次操作可以选择 a_i\leftarrow a_i\pm 1,求使 a 单调不降的最小操作次数
n\le 5\times 10^5,|a_i|\le 10^9
朴素 \mathrm{DP} 做法:
一个很显而易见的 \mathrm{DP},设 f_{i,j} 表示前 i 个数变成单调不降,最后一个数是 j 的最小操作次数,有转移:
f_{i,j}=\min_{k\le j}\set {f_{i-1,k}}+|a_i-j|
记 g_{i} 表示 f_i 的前缀 \min,有
g_{i,j}=\min_{k\le j}f_{i,k} \\
f_{i,j}=g_{i-1,j}+|a_i-j|
分析凸性:
记 F(x)=f_{i,x},G(x)=g_{i-1,x},有 F(x)=G(x)+|a_i-x|
由于 g 是前缀 \min,所以 G 是下凸函数,并且绝对值函数也是下凸函数,由此,两者的和 F 也是下凸的,换言之,f_i 是下凸的
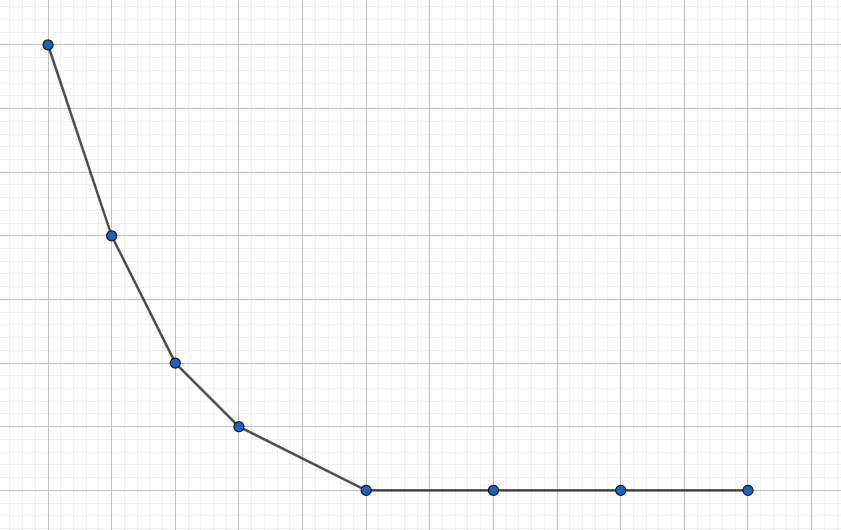
那么 $F$ 就是给位置 $x$ 加上 $|a_i-x|$,然后再求前缀 $\min$ 获得 $G
\mathrm{DP} 优化
用一个大根堆来维护所有的转移点,于是每次取出的堆顶就是最优答案的决策点
加上函数 |a_i-x| 相当于 a_i 前斜率全部 -1,后面全部 +1,相当于在转移点中加入 \set {a_i,a_i}
分讨一下,设堆顶的决策点为 op
① a_i\ge op,此时右边斜率全部 +1 在取 \min 后被全部推平,所以只用加 \set{a_i}
② a_i<op,此时 op 后半段会被加上去并在取 \min 后被全部推平,于是要弹出堆中,然后此时 a_i 会成为最优决策点,带回原来的 \mathrm{DP} 柿子,可以发现从 op 转移到 a_i,答案变化量为 op-a_i,于是更新答案,然后再丢进去 \set{a_i,a_i} 即可
例二:P3642 APIO2016 烟火表演 - 洛谷
定义 f_u(x) 表示 u 为根的子树内所有烟花都在 i 时刻燃爆的最少代价,易得转移:
f_u(x)=\sum_{v} (\min_{0\le i\le x}\set{f_v(i)+|w-(x-i)|})
很明显这是一堆绝对值函数的和,一定是一个下凸包
将后面的一部分表示出来
f^\prime(x)=\min_{0\le i\le x}\set{f_v(i)+|w-(x-i)|}
考虑 f^\prime 和 f_v 的关系
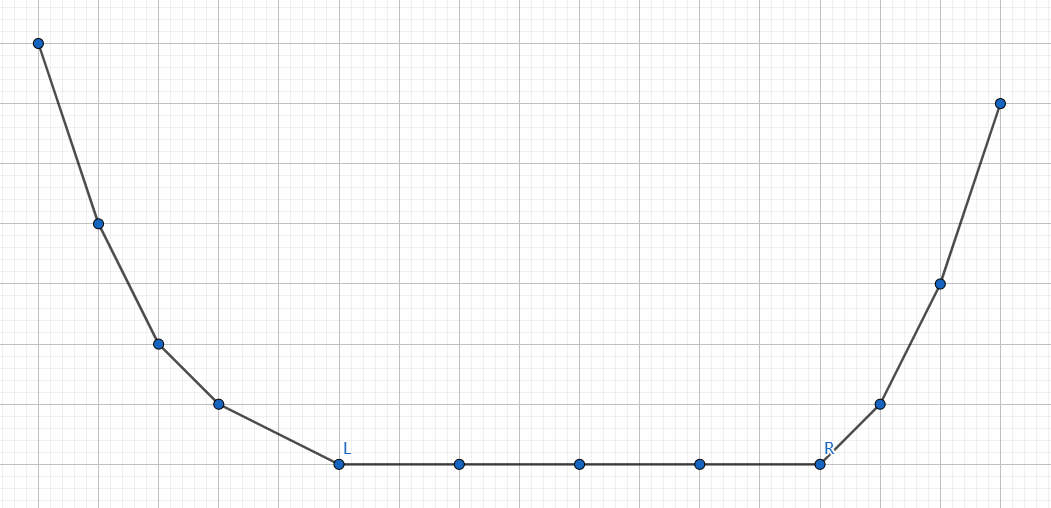
接下来分讨:
- $x\le L
此时让 i 取到 x 一定最优,f^\prime(x)=f(x)+w
-
L<x\le L+w
此时让 i 取到 L 一定最优,f^\prime(x)=f(L)+|w-(x-L)|=f(\min)+w-x+L
-
L+w<x\le R+w
此时让 i 取到 x-w 一定最优,f^\prime(x)=f(x-w)=f(\min)
-
R+w<x
此时让 i 取到 R 一定最优,f^\prime(x)=f(R)+|w-(x-R)|=f(\min)+x-R-w
可以发现操作对应了【向上平移 w 】、【变成一个斜率为 -1 的直线】、【 [L,R] 向右平移到 [L+w,R+w] 】、【变成一个斜率为 1 的直线】
因此拐点的变化只有删去 L,R 增加 L+w,R+w,于是用一个堆维护拐点,然后合并时使用左偏树 / 启发式合并合并拐点的堆。
然后我们得到了 1 号点的所有拐点的堆,考虑如何计算答案
由于 x\le L 的部分每次都会加上 w,所以 f_{1,0} 其实是所有边的边权和,于是我们根据存储拐点的堆的定义,每次弹出时减去就可以推出位于底层的答案。
例三:P11678 [USACO25JAN] Watering the Plants P
题解
闵可夫斯基和
理论
两个凸包的闵和可以看做是把一个凸包的顶点不断换成另一个凸包顶点后最外层组成的凸多边形,这里不详细展开,主要分析下凸壳时的情况。
闵和主要是用来优化 \left(\min,+\right) 卷积的一个方法,有重要性质:
两个下凸壳的 \left(\min,+\right) 卷积依然是一个下凸壳
假设要把下凸壳 f,g 做 \left(\min,+\right) 卷积,即要计算
h_i=\min_{j+k=i}\set {f_j+g_k}
那么此时
h 的差分数组就是 f,g 差分数组的归并
有这个重要性质,就可以考虑用平衡树等数据结构快速维护凸壳的差分数组
例题
例一:P9962 [THUPC 2024 初赛] 一棵树
题解
wqs二分
理论
wqs二分基于凸包。
常常用于强制选择 k 个满足某种属性的物品的最优化问题。
最优化问题转化成可行性问题,即判断是否选择 k 个。
设置一个偏移量 \Delta,对每个有限制的物品叠上 \Delta 进行影响,判断是否满足,然后二分,最后撤销 \Delta 得到答案。
例题
例一:P2619 [国家集训队] Tree I
简要题意: 给你一个无向带权连通图,每条边是黑色或白色。让你求 恰好有 K 条白色边 的 |\mathrm{MST}|。
分析:
最小生成树可以用Kruskal简单求解,但是此时强制要求选择 K 条白边,要分析性质。
定义 g_x 表示选择恰好 x 条白边时的 |\mathrm{MST}|,我们将 (x,g_x) 看做一个点放在平面直角坐标系里,可以发现这些点会构成一个下凸包,于是可以使用 wqs 二分。
我们要有一个办法来改变选择的白色边的数量,我们可以选择一个 \Delta,将所有白色边的权值都加上 \Delta,然后求这个新图的 |\mathrm{MST}|,假设选择了 k 条白边,如果 k\ge K,那么要选择少一点白边,让 \Delta 增加,否则让 \Delta 减少,由于刚刚分析的凸性,直接二分就可以找到 \Delta,然后减去加上的边权即可得到答案:ans=|\mathrm{MST}|-K\times \Delta。
例二:P4983 忘情
简要题意: 定义 a 的权值为 \left(\sum a_i+1\right)^2。
给定长度为 n 的序列 A,将其划分为恰好 m 段,权值定义为各段权值和,最小化权值。
分析:
先算出前缀和 s。
然后有一个显然的 \mathrm{DP},定义 f_{i,j} 表示前 i 个数划分为恰好 j 段的最小权值,有
f_{i,j}=\min_{k<j} \set {f_{k,j-1}+(s_i-s_j+1)^2}
可以用斜优,但是最多优化到 O(nm),考虑想办法分析性质优化掉 j。
由于 (a+b+1)^2\ge (a+1)^2+(b+1)^2,所以划分组数越多答案一定越小,因此设 g_x 表示划分为 x 组的答案,那么很明显 (x,g_x) 一定组成一个下凸包。
如果我们可以想办法影响最优解划分的组数,那么使用 \mathrm{wqs} 二分就可以解决了。
影响的方法也很简单,直接在每一次划分时加上一个划分代价 \Delta 即可,于是就可以先取消掉划分段数的限制进行 \mathrm{DP}。
f_i=\min_{j<i}\set{f_j+(s_i-s_j+1)^2+\Delta}
然后记录一个取到最优解时的划分段数 g,如果 g_n\le m 说明要划分更多,于是减少划分的代价,否则增加代价。
最后撤销代价,答案为 f_n-m\times \Delta。
其中 \mathrm{DP} 可以用斜率优化做到 O(n),所以总时间复杂度 O(n\log V)。