「CROI · R2」公交接驳

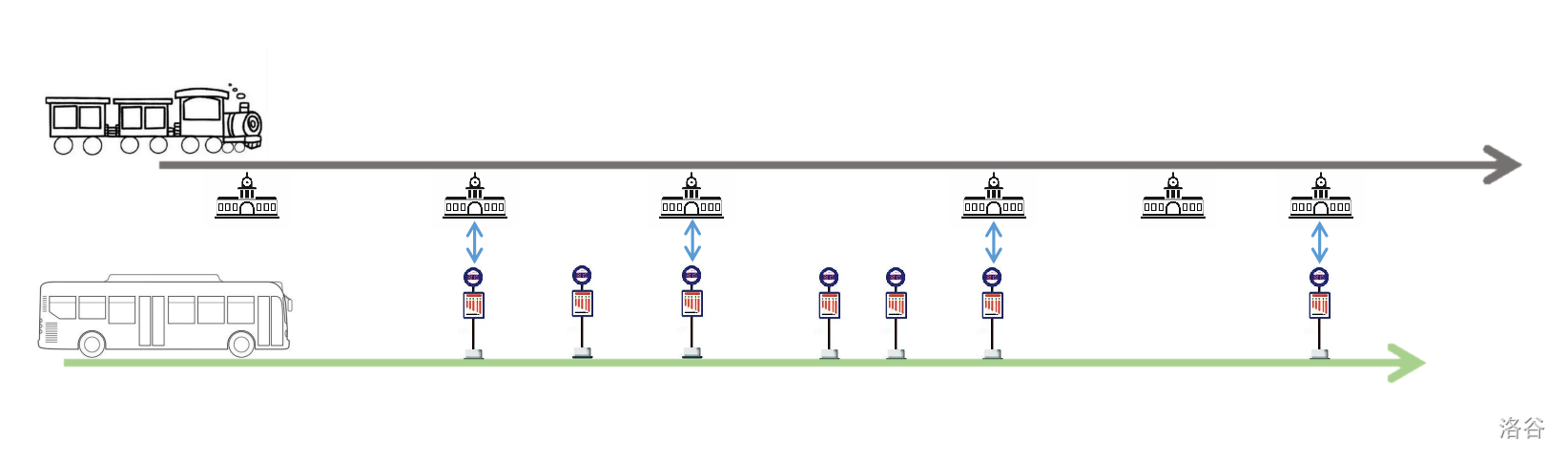
H 市是一座特大城市，每天来往于城市各个角落的乘客络绎不绝。该市郊区建筑分散，为方便周边群众出行，该市沿平行于主要公路的方向修建了市郊铁路，与公路上的公交系统形成互补格局。同一方向上的铁路站点与公交站点不完全一致，但设有若干个换乘站，铁路列车与公交车均停靠换乘站。现目前，市郊铁路仅在早高峰、晚高峰时各单向发一趟列车。  上图是沿早高峰方向的市郊铁路和公交车的停靠站点示意图。用蓝色箭头连接的为换乘站，市郊铁路的乘客可以在这些车站换乘公交车。 在下面的问题中，我们忽略非换乘站的存在，仅考虑换乘站在运营过程中的影响。

由于城市人口增多，H 市市郊铁路通勤压力增大，为了应对短时大客流，公交集团决定于早高峰时期在某条公交线路上安排若干班次的公交车，其运行方向与早高峰时期列车的开行方向相同，均为自西向东运行，便于乘坐火车的乘客换乘公交到达目的地。 给出一条共有 $n$ 个换乘站的街道，由西向东地将每个换乘站编号为 $1\sim n$。每一个换乘站的调度室对行驶效率的重视程度有所不同，第 $i$ 个换乘站的重视程度为 $v_i$。不同公交车在同一区间内的行驶时间相同，从第 $i$ 个换乘站行驶至第 $i+1$ 个换乘站的**时间**均为 $s_i$，可以忽略车辆停站的时间。市郊铁路列车到达第 $i$ 个换乘站的**时刻**为 $t_i$。保证两个换乘站之间乘坐公交车花费的时间一定不小于乘坐市郊铁路花费的时间。 现在你需要在这条公交线路上安排 $k$ 班公交车。全部的 $n$ 个换乘站都会有乘客从铁路下车。对于每一班车，你都需要安排其发车的时刻和发车的换乘站，且需要保证从任意一个换乘站下车的乘客均能坐上公交车，即最晚到达换乘站 $i$ 的公交车的到达时刻必须不小于 $t_i$。每班公交车发车后，都会以既定速度向东行驶至第 $n$ 个换乘站，并在途中的每个车站停靠并接上所有等候的乘客。你可以任意指定每条公交线路的始发站和发车时刻。 乘客们会登上他们到达车站后，首辆到达该站的公交车。定义换乘站 $i$ 的不满意度为在该站点处，于 $t_i$ 时刻从铁路下车的乘客等待首辆到达该站的公交车所花费的时间与乘客登上的公交车的始发站的重视程度的乘积。如果存在多班公交车同时到站，我们认为乘客登上的是始发站重视程度最小的一班。你需要最小化所有 $n$ 个换乘站的不满意度之和。 铁路时刻表和可供公交公司使用的空闲公交车数量总是在变化，所以你需要处理多组 $t_i$ 和 $k$ 不同的询问。

第一行包含一个正整数 $n$，表示换乘站的数量。 第二行包含 $n-1$ 个用空格隔开的非负整数 $s_1,s_2,...,s_{n-1}$。 第三行包含 $n$ 个用空格隔开的非负整数 $v_i$。 第四行包含一个正整数 $p$，表示不同市郊铁路时刻表的数量。 接下来共有 $p$ 组数据，每组数据包含三行。 每组第一行包含 $n$ 个用空格隔开的正整数 $t_1,t_2,\cdots,t_n$。 每组第二行包含一个正整数 $q_i$ ，表示在当前时刻表下询问的 $k$ 的数量。 每组第三行包含 $q_i$ 个用空格隔开的正整数 $k_1,k_2,\cdots,k_q$，表示询问的不同的 $k$。

输出 $p$ 行，每行 $q_i$ 个用空格隔开的正整数，表示在当前询问的 $k$ 的情况下，所有换乘站不满意度之和的最小值。

3
3 4
6 2 1
2
1 3 7
2
1 2
2 3 5
3
1 2 4

12 0
36 4 0

6
2 2 2 2 3
13 12 15 9 3 1
3
5 7 9 11 12 13
4
1 2 4 8
3 4 5 7 8 10
3
2 4 5
1000000 1000001 1000002 1000003 1000004 1000005
2
1 3

52 6 0 0
49 3 0
208 31

**【数据范围】** 对于所有测试点，保证 $1\leq n\leq 1000$，$1\leq p\leq 10$，$s_i\geq t_{i+1}-t_i\geq 0$，$1\leq q_i,k_i\leq 10^6$，$0\leq v_i,\sum s_i\leq 10^6$，$1\leq t_i\leq 2\times 10^6$。 本题采用捆绑测试。 | 子任务 | $n≤$ | $q≤$ | $k_i≤$ | $∑s_i≤$ | 特殊性质 | 分值 | | :----: | :----: | :----: | :----: | :-----: | :------: | :--: | | $1$ | $15$ | $1000$ | $1000$ | $15$ | 无 | $5$ | | $2$ | $15$ | $10^6$ | $10^6$ | $10^6$ | 无 | $5$ | | $3$ | $100$ | $10^6$ | $10^6$ | $10^6$ | 无 | $15$ | | $4$ | $1000$ | $10^6$ | $10^6$ | $10^6$ | $A$ | $5$ | | $5$ | $1000$ | $10^6$ | $10^6$ | $10^6$ | $B$ | $30$ | | $6$ | $1000$ | $1000$ | $1100$ | $1000$ | 无 | $10$ | | $7$ | $1000$ | $10^6$ | $10^6$ | $10^6$ | 无 | $30$ | 特殊性质 $A$：对于所有输入，保证 $s_i=t_{i+1}-t_i$。 特殊性质 $B$：保证 $v_i=1$。 **【样例解释】** 下面对于样例一的各询问给出一组可行的最优发车方案。注意可以使得答案最优的方案可能是不唯一的。 对于样例一的第一组时刻表： - 当 $k=1$ 时，我们于时刻 $1$ 在站点 $1$ 发车，具体运营信息如下表所示。 | | 车站 $1$ | 车站 $2$ | 车站 $3$ | | :-------------------: | :------: | :------: | :------: | | 市郊铁路到站时刻 | $1$ | $3$ | $7$ | | 公交班次 $1$ 到站时刻 | $1$ | $4$ | $8$ | | 乘客登上的班次 | 班次 $1$ | 班次 $1$ | 班次 $1$ | | 乘客等待时间 | $0$ | $1$ | $1$ | 班次 $1$ 的起点站为车站 $1$，$v_1=6$。故最终答案为 $6\times 0+6\times 1+6\times 1=12$。 - 当 $k=2$ 时，我们于时刻 $1$ 在站点 $1$ 发车，于时刻 $3$ 在站点 $2$ 发车，具体运营信息如下表所示。 | | 车站 $1$ | 车站 $2$ | 车站 $3$ | | :-------------------: | :------: | :------: | :------: | | 市郊铁路到站时刻 | $1$ | $3$ | $7$ | | 公交班次 $1$ 到站时刻 | $1$ | $4$ | $8$ | | 公交班次 $2$ 到站时刻 | / | $3$ | $7$ | | 乘客登上的班次 | 班次 $1$ | 班次 $2$ | 班次 $2$ | | 乘客等待时间 | $0$ | $0$ | $0$ | 班次 $1$ 的起点站为车站 $1$，$v_1=6$；班次 $2$ 的起点站为车站 $2$，$v_2=2$。故最终答案为 $6\times 0+2\times 0+2\times 0=0$。 对于样例一的第二组时刻表： - 当 $k=1$ 时，我们于时刻 $2$ 在站点 $1$ 发车，具体运营信息如下表所示。 | | 车站 $1$ | 车站 $2$ | 车站 $3$ | | :-------------------: | :------: | :------: | :------: | | 市郊铁路到站时刻 | $2$ | $3$ | $5$ | | 公交班次 $1$ 到站时刻 | $2$ | $5$ | $9$ | | 乘客登上的班次 | 班次 $1$ | 班次 $1$ | 班次 $1$ | | 乘客等待时间 | $0$ | $2$ | $4$ | 班次 $1$ 的起点站为车站 $1$，$v_1=6$。故最终答案为 $6\times 0+6\times 2+6\times 4=36$。 - 当 $k=2$ 时，我们于时刻 $2$ 在站点 $1$ 发车，于时刻 $3$ 在站点 $2$ 发车，具体运营信息如下表所示。 | | 车站 $1$ | 车站 $2$ | 车站 $3$ | | :-------------------: | :------: | :------: | :------: | | 市郊铁路到站时刻 | $2$ | $3$ | $5$ | | 公交班次 $1$ 到站时刻 | $2$ | $5$ | $9$ | | 公交班次 $2$ 到站时刻 | / | $3$ | $7$ | | 乘客登上的班次 | 班次 $1$ | 班次 $2$ | 班次 $2$ | | 乘客等待时间 | $0$ | $0$ | $2$ | 班次 $1$ 的起点站为车站 $1$，$v_1=6$；班次 $2$ 的起点站为车站 $2$，$v_2=2$。故最终答案为 $6\times 0+2\times 0+2\times 2=4$。 - 当 $k=4$ 时，我们分别于时刻 $-2$ 和时刻 $2$ 在站点 $1$ 发车，于时刻 $1$ 和时刻 $3$ 分别在站点 $2$ 发车，具体运营信息如下表所示。 | | 车站 $1$ | 车站 $2$ | 车站 $3$ | | :-------------------: | :------: | :------: | :------: | | 市郊铁路到站时刻 | $2$ | $3$ | $5$ | | 公交班次 $1$ 到站时刻 | $-2$ | $1$ | $5$ | | 公交班次 $2$ 到站时刻 | $2$ | $5$ | $9$ | | 公交班次 $3$ 到站时刻 | / | $1$ | $5$ | | 公交班次 $4$ 到站时刻 | / | $3$ | $7$ | | 乘客登上的班次 | 班次 $2$ | 班次 $4$ | 班次 $3$ | | 乘客等待时间 | $0$ | $0$ | $0$ | 班次 $1$ 和 $2$ 的起点站为车站 $1$，$v_1=6$；班次 $3$ 和 $4$ 的起点站为车站 $2$，$v_2=2$。故最终答案为 $6\times 0+2\times 0+2\times 0=0$。 值得注意的是，对于车站 $3$，班次 $1$ 和班次 $3$ 同时最早到达，但由于班次 $1$ 对应的重视程度 $v_1=6$，班次 $3$ 对应的重视程度为 $v_2=2$，因此乘客登上的是班次 $3$。