P6803 [CEOI 2020] 星际迷航
题目背景
原时空限制:0.2s,32m
题目描述
星际联邦由 $N$ 颗行星组成,分别编号为 $1 \sim N$。一些行星间由星际通道相连。通过这些星际通道,飞船可以在短时间内往返于各星球之间。整个星际联邦中恰好有 $N-1$ 条星际通道,并且通过这些星际通道,任意两颗行星之间均能相互抵达。
除了我们所处的宇宙之外,还有 $D$ 个平行宇宙,这些平行宇宙是我们的宇宙的完全复刻,它们的行星,星际通道都和我们的完全相同。我们将这些平行宇宙编号为 $1 \sim D$(我们的宇宙编号为 $0$),记第 $i$ 个宇宙的第 $x$ 颗行星为 $P_{x}^i$。通过星门,我们可以在这些平行宇宙间穿梭。$\forall i \in [0,D)$,我们将选择一个 $A_i$ 和一个 $B_i$(要求 $1 \leq A_i,B_i \leq N$),在 $P_{A_i}^i$ 和 $P_{B_i}^{i+1}$ 之间搭建一个**单向**(只能从 $P_{A_i}^i$ 前往 $P_{B_i}^{i+1}$)星门。
当所有的星门都准备就绪后,联邦星舰 Batthyány 号将会开始它的处女航,它目前正环绕着 $P_1^0$ 行星。Ágnes 舰长准备和 Gábor 中尉玩这样一个游戏:两个人交替选择星舰接下来前往的目的地,要求该目的地可以通过星际通道或星门直接抵达。他们希望每次前往的星球都是之前未抵达过的。即,如果星舰抵达了 $P_{x}^i$,他们将不再经过这个星球(但是可以抵达 $x$ 在其他平行宇宙中的相应星球)。由 Ágnes 舰长作为先手开始游戏,Gábor 中尉作为后手,当一位玩家在他的回合中,不能选择一个合法的目的地时,他就输掉了游戏。
舰长和中尉都是绝对聪明的,他们知道所有星际通道和星门的排布方案,并且他们每次都按照最优方案行动。你需要求出,有多少种布置星门的方案,使得作为先手的 Ágnes 舰长必胜?两种布置星门的方案是不同的,当且仅当存在一个整数 $i$,使得 $A_i$ 或 $B_i$ 不同。
输入格式
第一行两个整数 $N,D$,分别代表星际联邦拥有的行星数和平行宇宙的数量。
接下来 $N-1$ 行,每行两个整数 $u,v$,表示 $\forall i \in [0,D]$,$P_u^i,P_v^i$ 之间有星际通道相连。
输出格式
输出能使舰长必胜的星门布置方案数对 $10^9+7$ 取模的结果。
说明/提示
### 样例解释
共有 $3 \times 3=9$ 种本质不同的布置星门的方案,下面列出四种舰长必胜的情况。
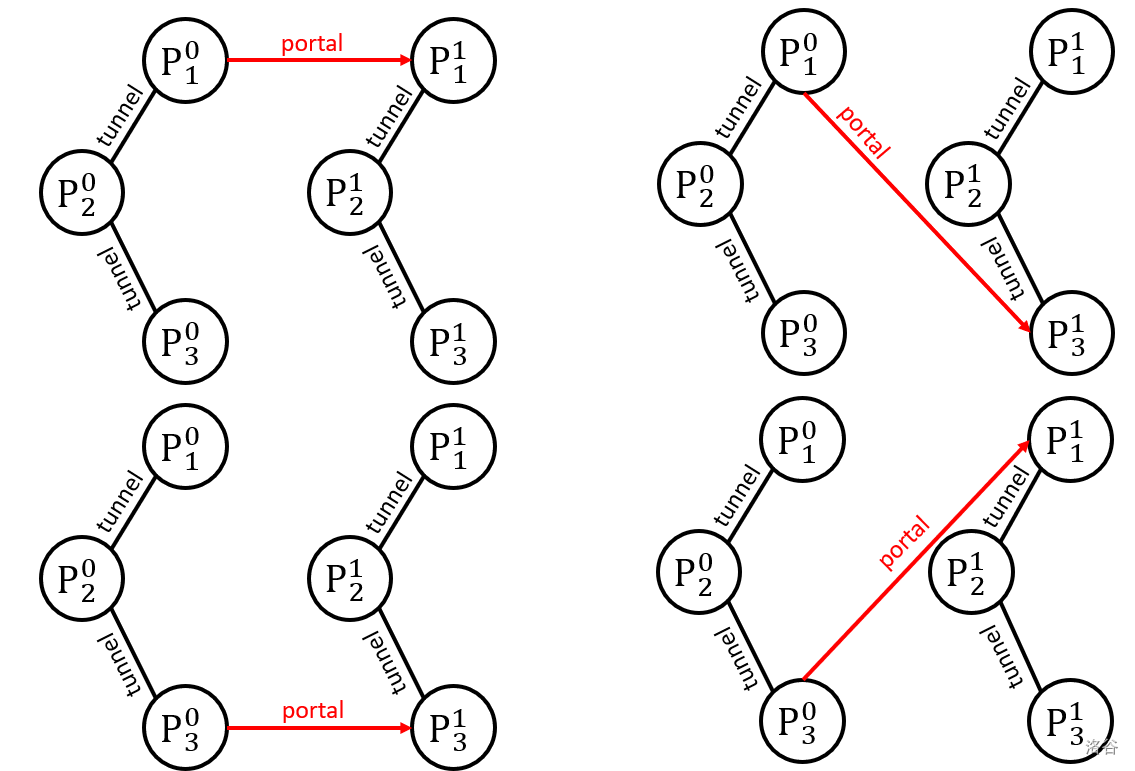
### 子任务
所有数据均满足:$1 \leq N \leq 10^5$,$1 \leq D \leq 10^{18}$,$1 \leq u,v \leq N$。
各子任务的约束条件如下:
| 子任务编号 | 分值 | 约束 |
| ---------- | ---- | ---------------------------- |
| $1$ | $0$ | 样例 |
| $2$ | $7$ | $N=2$ |
| $3$ | $8$ | $N \leq 100$,$D=1$ |
| $4$ | $15$ | $N \leq 1000$,$D=1$ |
| $5$ | $15$ | $D=1$ |
| $6$ | $20$ | $N \leq 1000$,$D \leq 10^5$ |
| $7$ | $20$ | $D \leq 10^5$ |
| $8$ | $15$ | 无特殊约束 |