二项式与二项式反演
题单介绍
## 二项式与二项式反演
### 二项式定理
$
(a + b)^n = \sum_{r=0}^{n} \binom{n}{r} a^{n-r} b^{r}
$
展开式具体形式为:
$
(a + b)^n = \binom{n}{0}a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^2 + \cdots + \binom{n}{r}a^{n-r}b^r + \cdots + \binom{n}{n}b^n
$
展开式特性:
1. **项数**:共 $ n + 1 $ 项。
2. **通项公式**:第 $ r + 1 $ 项为 $T_{r+1} = \binom{n}{r} a^{n-r} b^r$
其中 $ \binom{n}{r} $ 称为二项式系数,$ r $ 的取值范围为 $ 0 \leq r \leq n $。
### 例题:
1. 在$(1 + 2x)^{10}$中,求含$x^3$的项的系数大小。
2. 求$(x^2 + \frac{1}{x})^{8}$展开式中含$x^4$的项的系数大小。
## 二项式反演
对于数列来说,通过原数列计算出新的数列叫作演绎,而通过计算出的数列反推出原数列则被称为反演。
### 二项式反演常用形式:
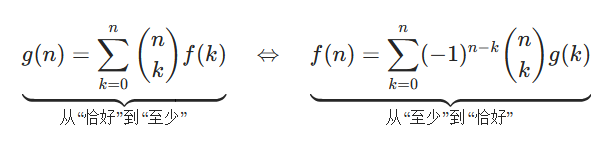
### 二项式反演更常用形式:

二项式反演的本质是通过二项式系数的正交性,借助$(−1)^k$的符号交替,在 “至少” 和 “恰好” 的计数之间建立可逆桥梁,是组合数学中解决容斥问题的关键工具之一。