二分图匹配

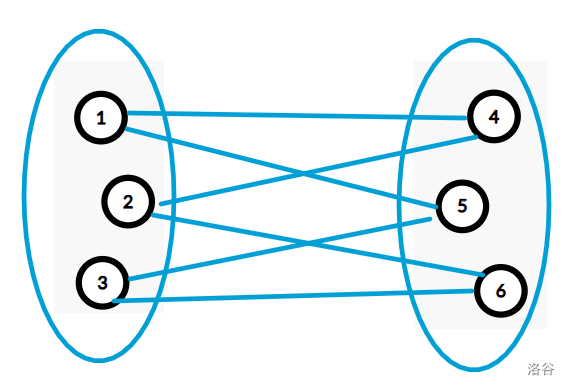
## 一、知识点讲解 ### 1. 二分图 * **定义**：若有无向图 $G=(U,V,E)$，且其顶点集 $U,V$ 可以分成两个子集合（注意这个无向图的所有边都连接着不同的子集里的两个点），则称无向图 $G$ 为一个二分图。 * **例如**：  $$图 1$$ 如图 $1$，这就是一个有 $6$ 个节点的二分图。 ### 2. 二分图匹配 #### （1）定义 * 若有一个无向图 $G=(U,V,E)$ 的边集里的某一条边都满足：这条边连接的两个节点只有这条边与其相连，则称此边为二分图匹配。 #### （2）匹配边与匹配点 * **匹配点**：两个已经匹配的点，称为匹配点。 * **匹配边**：连接一对匹配点的边，称为匹配边。 #### （3）最大匹配（重点，必看） * **定义**：若有一个匹配在一个二分图中含有边数最多，则称为这个二分图的最大匹配。 * **求法**： * 需要用到**匈牙利算法**，操作如下： * 对于一个左侧的节点 $a$，将 $a$ 的右侧的节点都遍历一遍，进行判断，找到能匹配的将其记录下来，然后继续查找下一个节点。 * 重复上一步即可。 * 增广路： * [百度百科的增广路，下面我讲的是一样的，但是清楚一点](https://baike.baidu.com/item/%E5%A2%9E%E5%B9%BF%E8%B7%AF/1332250?fr=ge_ala) * 若一个无向图中连接一对未匹配的点的边为 $W$，且此边上交替出现（即先是属于某点的边，然后是不属于此点的边，这两种边交替出现；也有可能先是不属于某点的边，然后是属于此点的边）的为属于某点的边以及不属于此点的边，则 $W$ 称为这个无向图中的增广路。 * 模板题 * [P3386 【模板】二分图最大匹配](https://www.luogu.com.cn/problem/P3386)（也是后面题单里的第一题） #### （4）完美匹配 * 若一个匹配边含有所有点，则称此匹配为完美匹配。 ## 二、题目说明 [P3386](https://www.luogu.com.cn/problem/P3386)和[P1559](https://www.luogu.com.cn/problem/P1559)是两道板子题；其他是我挑选的一些质量还算较高的题目，大部分需要用到别的算法，不过都比较简单（网络流除外，~~话说其实网络流我都没学过网络流~~）。