扫描线
题单介绍
# 扫描线算法(SLA)习题
## [算法讲解](https://zhuanlan.zhihu.com/p/103616664)[${\color{white}空格}$](https://handle.antfu.me/)洛谷没有的其他OJ的题可以去[VJ](https://vjudge.csgrandeur.cn/)提交
### 1. 模板题
| [T1 P1904](https://www.luogu.com.cn/problem/P1904) | [T2 P5490](https://www.luogu.com.cn/problem/P5490) | [T3 HDU1542](http://acm.hdu.edu.cn/showproblem.php?pid=1542) |
| :----------- | :----------- | :----------- |
### 2. 变形题
| [T4 P1856](https://www.luogu.com.cn/problem/P1856) | [T5 P1502](https://www.luogu.com.cn/problem/P1502) | [T6 HDU1255](http://acm.hdu.edu.cn/showproblem.php?pid=1255) | [T7 P3997](https://www.luogu.com.cn/problem/P3997) |[T8 HDU3642](http://acm.hdu.edu.cn/showproblem.php?pid=3642) |
| :----------- | :----------- | :----------- | :----------- |:----------- |
### 3. 圆的离散化与扫描线(选做)
| [T9 SPOJ8073](https://www.luogu.com.cn/problem/SP8073)/[BZ2178](https://darkbzoj.cc/problem/2178)( [_洛谷提交处_](https://www.luogu.com.cn/problem/T260588) ) | [T10 POJ1688](http://poj.org/problem?id=1688) | [T11 POJ1418](http://poj.org/problem?id=1418)|
|:----------- |:----------- |:----------- |
- - -
**T4:WA请看提示 $\quad$ T5:题目灵活 $\quad$ T6:题目两处更正见下 $\quad$ T7:我是飞行员舒克 $\quad$ T8:我是坦克手贝塔**
**T9-11:由于涉及计算几何许多难点,如自适应辛普森积分等,请依照自己的能力选做**
- - -
## 以下是 _简洁题面、题面翻译、题目更正、数据和数据范围、思路启发_
# T1 P1904 天际线(求拐点) [OwO](https://www.luogu.com.cn/problem/P1904) ✔
## 题目描述
所有的建筑用一个三元组 $(L_i,H_i,R_i)$描述,其中 $L_i$ 和 $R_i$ 分别是建筑的左坐标和右坐标,$H_i$ 就是建筑的高度。
用$x,y$ 坐标描述轮廓线上的折点
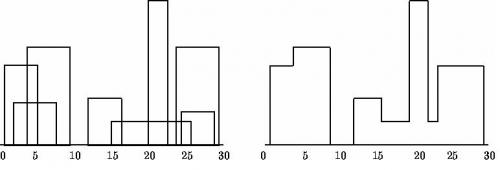
所有建筑的坐标中的数值都是小于 $10000$ 的正整数
至少有 $1$ 幢建筑,最多有 $5000$ 幢建筑
## 思路启发(已隐藏,框选可看)
第一级提示: {${\color{white}拐点与轮廓有什么关系?}$}
第二级提示: {${\color{white}一旦相邻坐标的轮廓高度发生变化,是不是会出现拐点?}$}
第三级提示: {${\color{white}如何使用堆求各个坐标的建筑的轮廓高度?}$}
第四级提示: {
${\color{white}堆忘光的话,找我要以前我讲过的堆的PPT吧?}$}
## 样例输入
```java
1 11 5
2 6 7
3 13 9
12 7 16
14 3 25
19 18 22
23 13 29
24 4 28
```
## 样例输出
```java
1 11 3 13 9 0 12 7 16 3 19 18 22 3 23 13 29 0
```
# T2 P5490 扫描线(求面积并)[OwO](https://www.luogu.com.cn/problem/P5490) ✔
## 题目描述
求 $n$ 个矩形的面积并。
**左下角坐标**为 $(x_1, y_1)$,**右上角坐标**为 $(x_2, y_2)$。
$1 \le n \le {10}^5$,$0 \le x_1 < x_2 \le {10}^9$,$0 \le y_1 < y_2 \le {10}^9$。
## 思路启发(已隐藏,框选可看)
第一级提示: {${\color{white}面积公式?}$}
第二级提示: {${\color{white}是不是当前块的总长(可能断开)乘以宽?}$}
## 样例输入
```java
2
100 100 200 200
150 150 250 255
```
## 样例输出
```java
18000
```
# T3 HDU1542 亚特兰蒂斯(求浮点面积并)[OwO](http://acm.hdu.edu.cn/showproblem.php?pid=1542) ✔
## Description
求 $n$ 个矩形的面积并。
**左下角坐标**为 $(x_1, y_1)$,**右上角坐标**为 $(x_2, y_2)$。
$1 \le n \le {100}$,$0 \le x_1 < x_2 \le {10}^5$,$0 \le y_1 < y_2 \le {10}^5$。
**保留两位小数**,每组数据输出后要**空一行**。
## Sample Input
```java
2
10 10 20 20
15 15 25 25.5
0
```
## Sample Output
```
Test case #1
Total explored area: 180.00
```
# T4 P1856 矩形周长(求周长)[OwO](https://www.luogu.com.cn/problem/P1856) ✔
## 题目描述
编写一个程序计算周长,矩形合并后的边长称为周长。
**左下角坐标**和**右上角坐标**
$1N<5000$ ,坐标的数值范围$-10000≤x,y≤10000$
温馨提示:本题配图即为样例图,这里不再展示
## 思路启发(已隐藏,框选可看)
第一级提示: {${\color{white}扫描线扫到边时总长的变化量代表着什么?}$}
第二级提示: {${\color{white}是不是觉得扫过一次矩形并不能很好地处理周长?}$}
第三级提示: {
${\color{white}试试扫两次来计算周长?}$}
WA提示: {
${\color{white}先处理出边还是先处理入边?重新定义的排序函数要体现}$}
## 样例输入
```java
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
```
## 样例输出
```java
228
```
# T5 P1502 窗口的星星 [OwO](https://www.luogu.com.cn/problem/P1502) ✔
## 题目描述
用矩形框点,使得所框的点的价值之和最大,求这个最大值
$T$ 组数据。$1\le T \le 10$
对于每组数据:
$n$ 颗星星,矩形长为 $W$,宽为 $H$。$1\le n \le 10^4$
$1\le W,H \le 10^6$
接下来 $n$ 行,点的坐标在 $(x_i,y_i)$,亮度为 $l_i$。$0\le x_i,y_i < 2^{31}$
## 思路启发(已隐藏,框选可看)
第一级提示: {${\color{white}在什么条件下星星才会出现在窗户中?}$}
第二级提示: {
${\color{white}当窗户的右上角端点的坐标出现在什么范围内时,星星会出现在窗户里?}$}
第三级提示: {
${\color{white}线段树树如何构造?是不是构造成max线段树更好?}$}
## 样例输入
```java
2
3 5 4
1 2 3
2 3 2
6 3 1
3 5 4
1 2 3
2 3 2
5 3 1
```
## 样例输出
```java
5
6
```
# T6 HDU1255 覆盖的面积(求面积交)[OwO](http://acm.hdu.edu.cn/showproblem.php?pid=1255) ✔
## Problem Description
给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.
**左下角坐标**和**右上角坐标** **(更正1)**
多测 $1≤T≤100$ ,$1≤N≤1000$ ,$0≤x,y≤100000$ ,浮点数,结果**保留两位小数**
## 思路启发(已隐藏,框选可看)
第一级提示: {${\color{white}扫描线模板应该怎么改?}$}
第二级提示: {${\color{white}由于线段树没有下推,能不能直接粗暴修改模板程序?}$}
第三级提示: {
${\color{white}如果对线段树新增一个属性行不行?应如何转移?}$}
WA提示: {
${\color{white}粗暴修改模板程序是不对滴哟?}$}
## Sample Input
```java
2
5
1 1 4 2
1 3 3 7
2 1.5 5 4.5
3.5 1.25 7.5 4
6 3 10 7
3
0 0 1 1
1 0 2 1
2 0 3 1
```
## Sample Output
**(更正2)**
```java
7.62
0.00
```
## 样例图
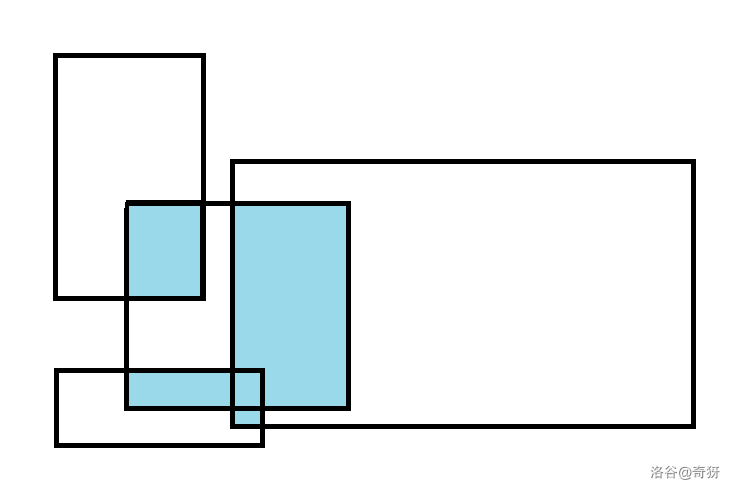
# T7 P3997 扇形面积并 [OwO](https://www.luogu.com.cn/problem/P3997)
## 题目描述
**(此处为同学们翻译成了角度制题面,洛谷题面为弧度制题面)**
给定 $n$ $(1\leq n\leq 10^5)$ 个同心的扇形,求有多少面积,被至少 $k$ $(1\leq k\leq 5000)$个扇形所覆盖。
## 输入格式
第一行是三个整数 $n$,$m$,$k$。$n$ 代表同心扇形个数,$m$ 代表将 $(−180^\circ ,180^\circ]$ 的角度区间平均分成 $2m$ 份。$(1\leq m\leq 10^6)$
从第二行开始的 $n$ 行,每行三个整数 $r,a_1,a_2$。描述了一个圆心在原点的扇形,半径为 $r$ $(1\leq r\leq 10^5)$,圆心角是从 $ \frac{a_1}{m}\times180^\circ$ 到 $ \frac{a_2}{m}\times180^\circ$ $(-m\leq a_1,a_2\leq m)$
## 输出格式
输出一个整数 $ans$ $(ans\leq 2^{63} - 1)$ ,$\frac{\pi}{2m}\times ans$ 等于至少 $k$ 个扇形所覆盖的总面积。
## 样例 #1
### 样例输入 #1
```java
3 8 2
1 -8 8
3 -7 3
5 -5 5
```
### 样例输出 #1
```java
76
```
## 样例 #2
### 样例输入 #2
```java
2 4 1
4 -4 2
1 -4 4
```
### 样例输出 #2
```java
98
```
## 思路启发(已隐藏,框选可看)
第一级提示: {${下面的推式子部分(隐藏后不方便阅读)}$}
### 推式子
$\boxed{记 {\theta}=\frac{360}{2m} }$
$({\theta}是单位角度,指把360^\circ分成2m份后,一份的角度)$
$\boxed{\therefore S_⌔=\frac{n\pi r^2}{360}=\frac{n\pi r^2}{2m{\theta}}=\frac{\frac{n}{{\theta}}\pi r^2}{2m}}$
$\boxed{\because S_⌔=ans \times \frac{\pi}{2m}}$
$\boxed{\therefore ans=\frac{n}{{\theta}}r^2 \quad
(\frac{n}{{\theta}},r\in\mathbb{N})}$
$\boxed{\therefore ans\in\mathbb{N}}$
$\boxed{\because |a_1-a_2|=\frac{n}{{\theta}}}$
$\boxed{\therefore ans=|a_1-a_2|r^2}$
# T8 HDU3642 找金库 [OwO](http://acm.hdu.edu.cn/showproblem.php?pid=3642)
## 题目大意
给出一个三维坐标系,给出n个立方体,求立方体**体积交**。
$n(1 ≤ n ≤ 1000)$,
$x1, y1, z1, x2, y2 ,z2$
$x,y ≤ 10^6 , z ≤ 500$.
## Sample Input
```java
2
1
0 0 0 5 6 4
3
0 0 0 5 5 5
3 3 3 9 10 11
3 3 3 13 20 45
```
## Sample Output
```java
Case 1: 0
Case 2: 8
```
# T9 SPOJ8073/BZ2178 圆并 [O](https://www.luogu.com.cn/problem/SP8073)w[O](https://darkbzoj.cc/problem/2178) [T260588](https://www.luogu.com.cn/problem/T260588)
## 题目大意
求n个圆的面积并
答案保留三位小数。
$N(1 \leq N \leq 1000)$表示圆的数量
圆的坐标与半径$X,Y,R$$(0 \leq |X|,|Y|,R \leq 1000)$。
注意:圆的半径可能为$0$,此时这个圆表示一个点
## Input:
```java
3
0 0 1
0 0 1
100 100 1
```
## Output:
```java
6.283
```
# T10 POJ1688 海豚池 [OwO](http://poj.org/problem?id=1688)
## 翻译后描述
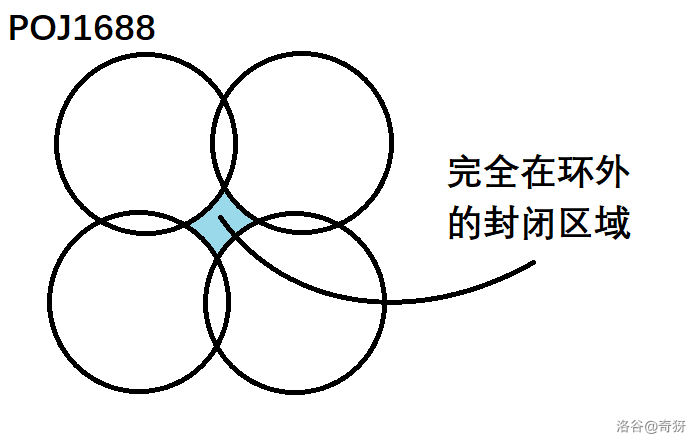
将几个塑料环扔进池中,使**任何环的中心位于任何其他环内**,并且**没有两个环相切**。计算**完全在环外的封闭区域**的数量(环之间的闭合区域数)。
$T (1≤T≤20)$
$N (1≤N≤20)$,
$X,Y,R$
($X,Y,R\in\mathbb{N},\ X,Y<1000,\ 1≤R≤100$)
## Sample Input
```java
2
4
100 100 20
100 135 20
135 100 20
135 135 20
1
10 10 40
```
## Sample Output
```java
1
0
```
# T11 POJ1418 五彩纸屑万岁 [OwO](http://poj.org/problem?id=1418)
## Description
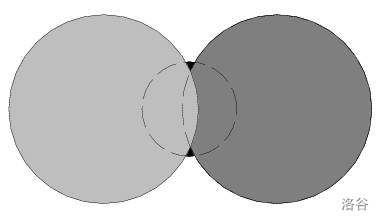
给定一堆圆,求可见的圆有几个。
$n$ $(n≤100)$
$x1\ y1\ r1(底部)$
$x2\ y2\ r2$
$...$
$xn\ yn\ rn(顶部)$
(多测,结束:$n=0$)
小数点后最多$12$位。不精确裕度为$± 5 \times 10^{-13}$。也就是说,保证输入值小于$± 5 \times 10^{-13}$的变化不会改变可见的圆。圆中包含的所有点的坐标在$-10$和$10$之间。
## Sample Input
```java
3
0 0 0.5
-0.9 0 1.00000000001
0.9 0 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 -0.00001 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 0 1.00000000001
2
0 0 1.0000001
0 0 1
2
0 0 1
0.00000001 0 1
0
```
Sample Output
```java
3
5
4
2
2
```