【图论】拓扑排序专题训练

首先，有这个题单是因为 NOIP 2020 的第一题考到了拓扑排序，并且似乎题单区并没有这个题单的说（ 其次，也写了学习笔记，也当自己的任务计划训练一下吧。 目前是 13 道题，如果再看到值得刷的题目还会新增，欢迎私信。 ## 题目简述 - P4017 最大食物链计数：很板子的题 - P6145 [USACO20FEB]Timeline G：差分约束$\to$ DAG，拓扑排序（SPFA 亦可） - P2419 [USACO08JAN]Cow Contest S：不是很显然的感觉，拓扑排序+并查集 - P7113 排水系统：拓扑排序+分数处理 - P1960 郁闷的记者：板板板板板 - P1137 旅行计划：先拓扑排序再 DP - P6154 游走：期望，拓扑排序 ## All Problems - [P4017 最大食物链计数](https://www.luogu.com.cn/problem/P4017) - [P2712 摄像头](https://www.luogu.com.cn/problem/P2712) - [P6145 [USACO20FEB]Timeline G](https://www.luogu.com.cn/problem/P6145) - [P1960 郁闷的记者](https://www.luogu.com.cn/problem/P1960) - [P2419 [USACO08JAN]Cow Contest S](https://www.luogu.com.cn/problem/P2419) - [P1137 旅行计划](https://www.luogu.com.cn/problem/P1137) - [P6154 游走](https://www.luogu.com.cn/problem/P6154) - [P1038 [NOIP2003 提高组] 神经网络](https://www.luogu.com.cn/problem/P1038) - [P4316 绿豆蛙的归宿](https://www.luogu.com.cn/problem/P4316) - [P1347 排序](https://www.luogu.com.cn/problem/P1347) - [P3275 [SCOI2011]糖果](https://www.luogu.com.cn/problem/P3275) - [P4742 [Wind Festival]Running In The Sky](https://www.luogu.com.cn/problem/P4742) - [P3243 [HNOI2015]菜肴制作](https://www.luogu.com.cn/problem/P3243) ----- $$\Large\color{cadetblue}\boxed{\textbf{从平面到线性：拓扑排序の降维打击}}$$ $$\small\underline{\rm Topological\ Sort:The\ Progress\ of\ Dimensionality\ Reduction}$$ 事实上，拓扑排序就是将一个图变化为一个线性序列的过程。 故，我愿称之为降维打击。 ## 壹：初识 我们依然按照网上一贯的方式引入，假设一中有以下 $n$ 个课程，在这个例子中我们令 $n=5$。 - $1.$ 珂学专项研究 $\rm Null$ - $2.$ 物理竞赛 $1,5$ - $3.$ 生物竞赛 $1$ - $4.$ 信息学电竞 $1,2,5$ - $5.$ 修电脑 $1$ 在每一项前的数字是他们的编号，而在他们后面的数字则是 **前置课程**，换言之，要想学 $x$ 课程，就必须把他所有的前置课程学完（其中如果是 $\Null$ 则没有前置课程）。那么，我们需要安排出一个学习顺序，怎么办呢？ 先随便选一个试试看吧！看着信息学电竞就觉得很有意思诶，看看：要先学这么多？？那看看前置课程中的修电脑罢……诶，也有前置课程？看看前置课程珂学研究——终于没有前置课程了！可以从这里开始学。那么，**没有前置课程** 的内容就是我们要先开始学的内容了。 那么，我们可以把**所有**没有前置课程的内容先学完。这里有一个重要的“删除”操作：如果我学过了 $x$ 课程，那所有课程中，如果有前置课程为 $x$ 的，可以把这个前置课程删掉了。为什么呢？因为已经学过了，相当于不再起作用；换言之，我们安排过学习顺序的课程就无需再学了，于是可以删掉。 那么学完珂学研究之后，课程变成了这样： - $2.$ 物理竞赛 $5$ - $3.$ 生物竞赛 $\rm Null$ - $4.$ 信息学电竞 $2,5$ - $5.$ 修电脑 $\rm Null$ 这时候我们发现 $3,5$ 都可以学了（没有前置课程），那么就学吧！学完之后，课程就变成了这样： - $2.$ 物理竞赛 $\rm Null$ - $4.$ 信息学电竞 $2$ 诶，$2$ 已经没有前置课程了！此时可以学习第二个课程，再学完后就变成了这样： - $4.$ 信息学电竞 $\rm Null$ 那么就可以学习信息学了！这是最后一个课程；至此，我们学课程的顺序如下： $$\rm Order=\{1,3,5,2,4\}$$ 对于这样的一个可行的顺序，我们称之为“拓扑序”，由于在同时有多个前置为零的课程时，选任何一个都可以（不影响结果），所以拓扑序可能有多种多样的结果，这不影响我们选课（对吧）。 诶，已经都没有前置课程了！那么就都学吧，先学前面的或者后面的都不影响（想一想，为什么），所以一种可行的学课程顺序是这样的： $$\rm Order=\{1,3,5,2,4\}$$ 这样的一个可行的顺序，我们称之为“拓扑序”，由于在同时有多个前置课程时，选任何一个都可以（不影响结果），所以拓扑序可能有多种多样的结果，这不影响我们选课（对吧）。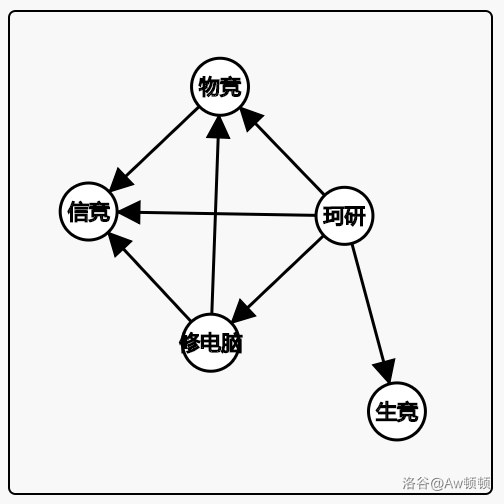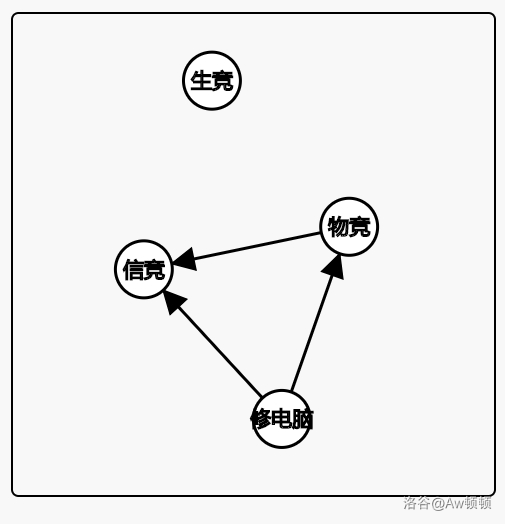 那么我们可以把这个过程抽象成一个图论的模型： - **前置课程** $\to$ **入度** - **课程** $\to$ **节点** 那么上面的课程就可以抽象成这样（箭头从前置课程指向下一个课程）：  那么我们学完珂研之后就变成了这样：  接下来的过程也显然简单不少（以此类推就行了）。 但是不如设想一个极其简单的场面（纯属虚构）： - “要想学线段树先学树状数组” - “要想学树状数组先学线段树” 那你会发现，当你想学那个常数大的东西时要先学树状数组，想学树状数组又要学线段树……这不是陷入死循环了么？其实，当这个图**存在环**时是不能进行拓扑排序的（原因如上），所以，能跑拓扑排序的一定是一个无环图，而且还得是一个有向图，那么，综合起来就是： $$\small\textbf{有向无环图（DAG, Directed Acyclic Graph）}$$ ----- ## 贰：实现 关键在于，哪些点是 **入度为 $0$** 的呢？ 我们的关键在于**维护一个入度为零的集合**。 当我们要删除一个节点 $x$ 的时候，就要进行“删除”操作，即删除和 $x$ 相关的所有边——事实上，由于我们对 $x$ 进行了操作，所以他必然入度为 $0$，删除的边全部都是出边。 这完了么？其实并没有——当你删除这些边时，他们指向的节点入度就减一了，这时，我们要把入度减一后为 $0$ 的节点放到集合中，这就成功地维护了一个集合。 那么我们来做一下例题吧。 ----- ### [HDU 1285 确定比赛名次](http://acm.hdu.edu.cn/showproblem.php?pid=1285) 以下为不改变题意的简化版描述。 有 $n$ 个编号为 $1,2\cdots,n$ 的队伍（$1\le n\le 500$），现要将他们从前往后排名，但不能直接获得每个队的比赛成绩，只知道每场比赛的结果，形如 $P_1$ 赢 $P_2$，意味着 $P_1$ 排名在 $P_2$ 前，求比赛的名次。 多测，每组第一行为 $n,m$，表示有 $n$ 个队 $m$ 场比赛，接下来 $m$ 行每行两个整数 $P_1,P_2$ 即 $P_1$ 赢了 $P_2$。 要求给出一个合理的排名，输出时队伍号之间有空格，最后一名后面没有空格。 其他说明：排名可能不唯一，故要求输出时编号小的队伍在前；输入数据保证有解。 Sample Input ~~~ 4 3 1 2 2 3 4 3 ~~~ Sample Output ~~~ 1 2 4 3 ~~~ 抽象化是一个重要的工具。 这时候我们考虑：如果 $P_1$ 胜过了 $P_2$，就划定一条从胜者指向败者的边，这样子，只要入度为 $0$ 就一定是“没有输过的人”，即第一名，接着按拓扑排序的思想来就行力。由于我们可以再找入度为 $0$ 节点时从前往后找，也可以保证“从小到大”这一条件。 ~~你说这出题人为了省 SPJ 就麻烦做题人呗~~ 那么我们约定一下变量名字： - $in$ 存储入度，$in_x$ 即 $x$ 节点的入度（前驱数量） - $mp$ 存储边（布尔类型），$mp_{(x,y)}$ 即 $x$ 和 $y$ 是否存在一条边 - $n,m$ 如题意所示。 - $q$ 存储拓扑排序路径的队列。 那么我们需要循环找到**入度为零**且**编号最小**的节点 $s$，入队。然后就可以处理：首先将其入队并把其入度赋值为 $-1$（想一想，为什么），然后再把前驱为他的所有节点入度减一，并删去相连的边。 多测记得清空，不知道为啥要防重边，鉴于细节有点多，还是放一下参考代码供大家对拍啥的。 ```cpp #include<bits/stdc++.h> using namespace std; bool mp[505][505];//存边（是否存在） int in[505],n,m;//存入度，以及两个变量 queue<int>q;//存拓扑排序后路径 void print(){ //鉴于奇怪的输出要求，决定写个输出函数 printf("%d",q.front()); //输出第一个 q.pop();//出队 while(!q.empty()){ printf(" %d",q.front());//输出 q.pop();//出队 }puts("");//换行 }void topo(){ for(int i=1;i<=n;i++){ int s;//找到编号最小的、入度为 0 的节点 for(int j=1;j<=n;j++){ if(in[j]==0){ //找出前驱数量为零的的点 s=j; break; } }q.push(s);in[s]=-1;//将第一名的前驱数量设为-1 for(int j=1;j<=n;++j){ //将相关（前驱为 s）的点处理 if(mp[s][j]){ in[j]--;//入度减 1 mp[s][j]=0;//删掉这条边 } } }print();//输出 }int main(){ while(cin>>n>>m){ memset(in,0,sizeof(in));//初始化 memset(mp,0,sizeof(mp)); for(int i=0;i<m;i++){ int x,y;cin>>x>>y; if(mp[x][y]==0){ //避免重复的数据输入 mp[x][y]=1; // in[y]++;//前驱数量加一 } }topo(); }return 0; } ```