平衡树
题单介绍
(该知识点较难,且容易写错,建议使用STL里的set作为代替)
前置知识:二叉排序树。
为了使二叉查找树在查找、插入、删除等操作时的时间在最坏情况下不会太长。也就是说,树的高度不要太高。于是我们要想办法尽量使这棵树左右平衡而使得它高度变小。
第一种方法,就是让这棵树的每一个子树都平衡,也就是左边和右边的子树的高度相差最多不超过1。
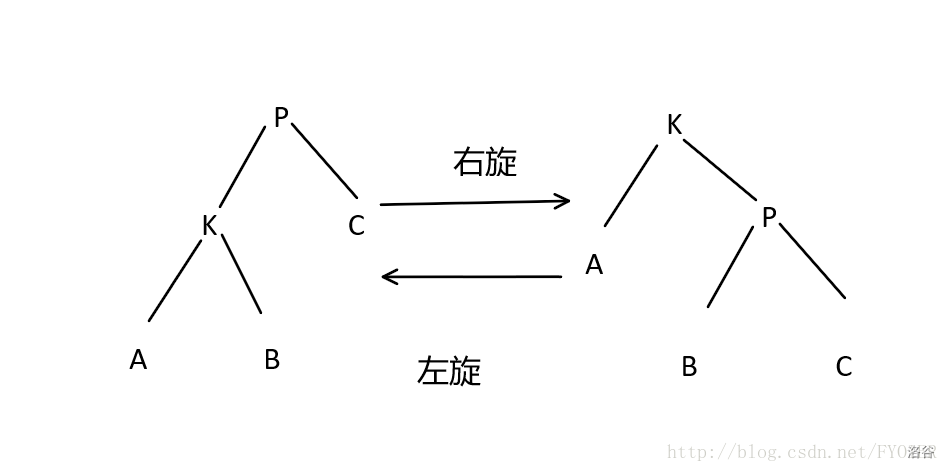
如果在插入或删除节点时某棵子树的两边不平衡了,就想办法让它旋转,使其平衡。
我们把这种数据结构称作AVL树,它能保证任何时刻树的高度不会超过O(log n)。
第二种方法,就是在概率上平衡。也就是说,使这棵树的期望高度不超过O(log n)。
为了达到这个目的,我们给每个节点一个新的值x。并且使每个节点的x都大于他的所有子节点。(类似堆的性质)
若某一对相连的节点不符合这个性质,那么就将其旋转使得父子关系互换。
我们称这种数据结构为Treap。
第三种方法,就是想办法使其在执行大量操作后,他的平均复杂度不超过O(log n)。
为了达到这个目的,我们在找到某个节点的位置后,先将其旋转至根节点,再对它进行操作。
我们称这种数据结构为伸展树(Splay)。可以证明它的操作的平均复杂度不超过O(log n)。
[Splay复杂度的势函数证明法](https://www.cnblogs.com/Mr-Spade/p/9715203.html)
这三种数据结构都用到了旋转操作,来调节树的高度,以及节点之间的位置关系。