【提高】二叉堆/优先队列应用

# 二叉堆和优先队列的应用 > 一个简单的数据结构，可能会产生绝对不同的效果。 ## 基础知识 二叉堆是一种特殊的堆，二叉堆是**完全二叉树**或者是**满二叉树**。二叉堆有两种：大根堆和小根堆。其差别仅在与**根节点（父节点）大小**和**左右子节点**的关系，因此，我们可以利用堆来完成**排序**及**查找**的工作。 普通队列的特性是先进先出的数据结构，元素在队列尾被加入，而从队列头弹出。在优先队列中，根据一定的标准（基本的是数字的大小）被赋予不同的**优先级**，当访问元素时，具有最高优先级的元素位于队首。优先队列属于 STL ，**通常采用堆数据结构来实现**。 ## 二叉堆の特性 对于两种不同的堆：小根堆和大根堆，分别对应“堆顶最大”“堆顶最小”，对于大根堆而言，任一非根节点的优先级都小于堆顶，反之任一非根节点的优先级都大于堆顶，注意，**根节点就是堆顶**。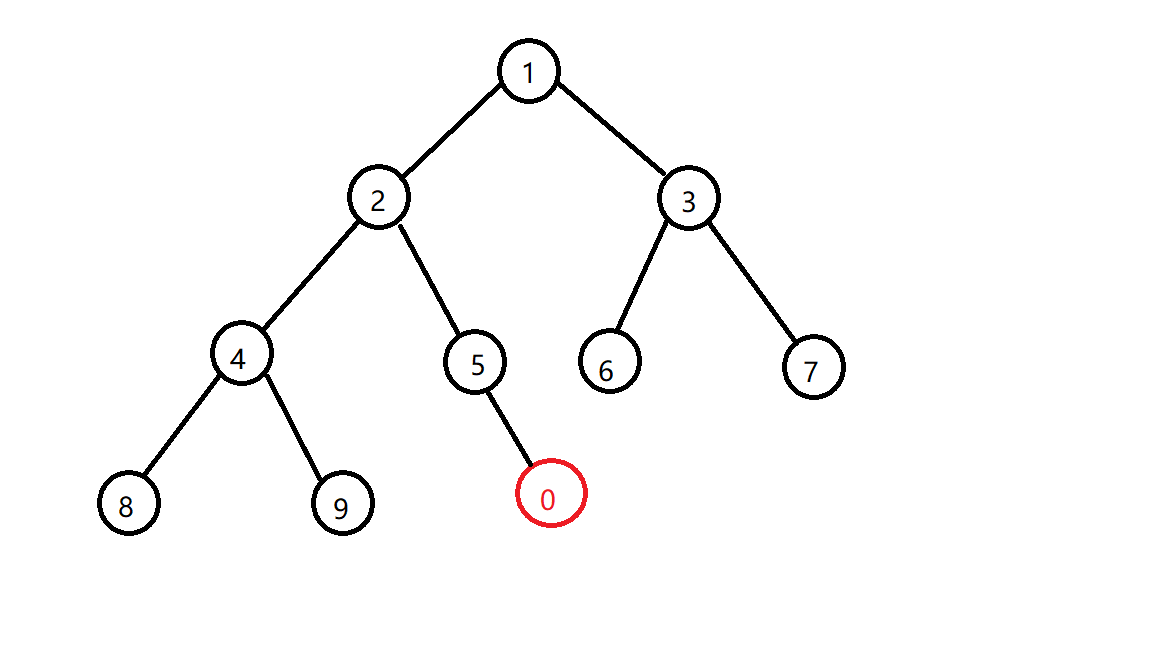 ## 二叉堆的操作 - ### 插入 $\bold{insert}$： 假设你已经有一个堆了:  假设你要插入 $0$ 。 先插到堆底，然后你会发现它比它的父亲小，不符合小根堆的性质了啊，那么从堆底一步步往上更新，若不符合规定就交换，但是，对于每一个叶子结点，我们都需要这么操作，直到确认这个堆完全有序为止。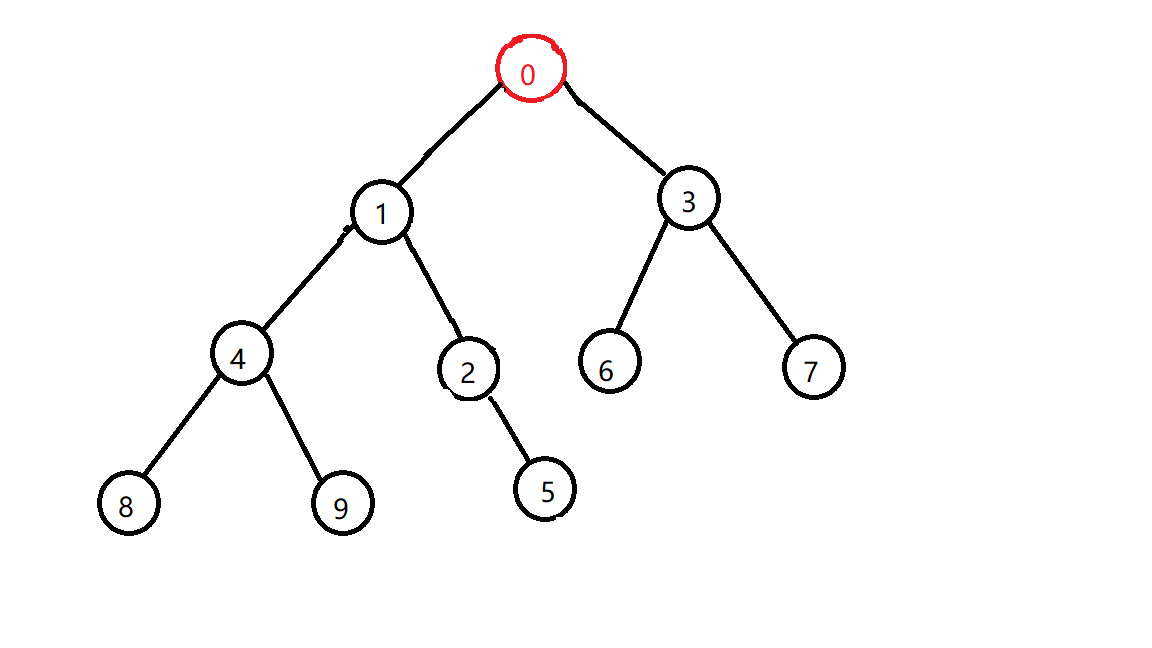 最后，排序结束后的二叉堆如下：  其实就是将叶子结点一个个和他们的父节点比对，像是把他们推上去，推到无需推动即可。 - ### 删除 $\bold{delete}$： 假设我们现在需要删除 $0$ （因为操作步骤较多，比较好讲解和理解）。 请注意，在删除的过程中还是要维护小根堆的性质，那么我们是否可以用与插入类似的方法？ 切勿直接删掉，因为这样，缺失了一个节点，那么这个堆就彻底混乱了，也无法继续进行接下来的操作。我们要保证能够好好维护这个堆。 其实方法也特别简单，刚刚是把他推上去，现在是把他拉下来。 我们只需要： - 把他和他的左右儿子比较，和小的那个换，这样就下移了一层。 - 接着，更新两者的下标，重复上述过程。 - 直到他已经没有儿子了，那么将他父亲对于他的下标改成 $\INF$ 或者 $0$。 请注意，这时候根节点的下标是从 $1$ 开始的，如果是 $0$ ，读者可以自己想一想其他的下标是什么情况。 - ### 查询 $\bold{find}$： 这其实是很简单的： 从头到尾，我们都维护了这个堆的性质，一切的操作都基于这种性质之上，所以我们只需要查询 `heap[1]` 就可以获得优先级极端的某个元素，当然，这种特性在优先队列也存在，而且码量明显降低，所以，牺牲一定的运行时间，来使用优先队列从而增加自己考场思考和优化的时间，在某种意义上来说是值得的。 ## 优先队列的基操 在学习基本操作的前提下，我们可以了解一下他的特性： 定义优先队列的代码实现： ```cpp #include<queue> priority_queue<int> q; priority_queue<int,vector<int>,greater<int> >q; ``` 当中第一个是大整数优先，后一个相反，注意结尾的 `> >` 有一个空格，否则系统为认为是位运算 `>>` 。 他有这些内置的函数： ```cpp q.top()//返回一个队头的值（最大或者最小） q.pop()//弹出队头元素 q.push()//插入元素并保持其特性 q.empty()//查询是否为空，为空返回1，反之返回0 q.size()//查询堆内元素数量 ``` 这些是比较常见的操作，用不到 20% 代码实现了 100% 的功能。 ## 时间复杂度 因为堆是一棵完全二叉树，所以对于一个节点数为 $n$ 的堆，它的高度不会超过 $\log_2 n$ 所以对于插入，删除操作复杂度为 $O(\log n)$。 查询堆顶操作的复杂度为 $O(1)$。 ## 堆及优先队列的应用 ### 1. 排序 这是最基础的功能。 其实就是用要排序的元素建一个堆，然后依次弹出堆顶元素，最后得到的就是排序后的结果了 但是我们的 STL 有 `sort` 且实践复杂度其实是比快排和堆排的 $O(n\log n)$ 更优的，所以不建议为了排序写一个堆。 ### 2. 查询第 $k$ 大的元素 利用一个大根堆一个小根堆来维护第 $k$ 小。 直接读入所有元素，枚举询问，把前面的第 $k$ 个元素都放进大根堆里面，然后如果元素数量大于 $k$，就把堆顶弹掉放到小根堆里面，使大根堆的元素严格等于 $k$，这样这次询问的结果就是小根堆的堆顶了（前面 $k-1$ 小的元素都在大根堆里面了） 但是 STL 是个东西，全部 `push` 进去，然后 `pop` $k-1$ 次，直接输出队头即可，复杂度差不多是 $O(k\times n\log n)$ 这样子？ 所以，还是建议用优先队列。 ## 课后习题 本次的题目难度由浅入深，适合新手和大佬们切题。 当然，当中不一定带有 `优先队列` 和 `二叉堆` 的标签，因为在比较简单的排序工作中，我们也可以利用他们，所以可能在保证代码连贯性的时候会使用这种容器。 不过，最后要说的是，在难度越来越提升的题目中，STL 容器和手写堆的用处越来越被弱化，其实在当中扮演的角色也绝非主要，但是他们对于减小码量和提高代码可读性甚至于方便调试都可以起到至关重要的作用。 最后，祝大家刷题愉快！ ## $\bold{Reference}$ **[henry_y の 浅析基础数据结构-二叉堆](https://www.cnblogs.com/henry-1202/p/9307927.html)** **[江无羡 の 二叉堆(最小堆, 最大堆)介绍与实现](https://blog.csdn.net/HinstenyHisoka/article/details/91817687)** ## 练习题目 - [P1334 瑞瑞的木板](https://www.luogu.com.cn/problem/P1334) - [P1628 合并序列](https://www.luogu.com.cn/problem/P1628) - [P1177 【模板】快速排序](https://www.luogu.com.cn/problem/P1177) - [P3378 【模板】堆](https://www.luogu.com.cn/problem/P3378) - [P1090 [NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G](https://www.luogu.com.cn/problem/P1090) - [P1878 舞蹈课](https://www.luogu.com.cn/problem/P1878) - [P4058 [Code+#1]木材](https://www.luogu.com.cn/problem/P4058) - [P1168 中位数](https://www.luogu.com.cn/problem/P1168) - [P1631 序列合并](https://www.luogu.com.cn/problem/P1631) - [P2085 最小函数值](https://www.luogu.com.cn/problem/P2085) - [P1325 雷达安装](https://www.luogu.com.cn/problem/P1325) - [P1491 集合位置](https://www.luogu.com.cn/problem/P1491) - [P2707 Facer帮父亲](https://www.luogu.com.cn/problem/P2707) - [P4296 [AHOI2007]密码箱](https://www.luogu.com.cn/problem/P4296) - [P5032 经验](https://www.luogu.com.cn/problem/P5032) - [P1954 [NOI2010] 航空管制](https://www.luogu.com.cn/problem/P1954) - [P4404 [JSOI2010]缓存交换](https://www.luogu.com.cn/problem/P4404) - [P5283 [十二省联考2019]异或粽子](https://www.luogu.com.cn/problem/P5283) - [P3766 核心密码B](https://www.luogu.com.cn/problem/P3766)